Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 13

а)Якщо крива L задана рівнянням , то  при  маємо 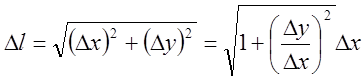 тому          .

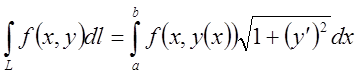                                                  (7.7)

б)Якщо крива L задана рівнянням , то  і при  одержимо

                                

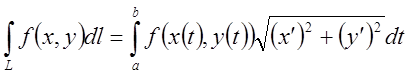
Якщо крива інтегрування задана в трьохвимірному просторі , то формули обчислення інтегралів другого і першого типу мають вид

          

   

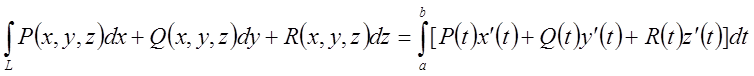
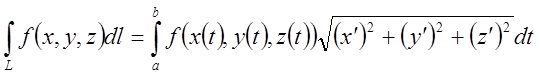
3). Формула Гріна.

 Теорема. Якщо функції P(x,y)  і Q(x,y) неперервні разом зі своїми частинними похідними в замкнутій обмеженій області D, то має місце формула

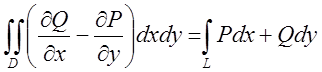
10.7. Вправи на засвоєння матеріалу.

1).  Розв’яжемо декілька прикладів:

 ПРИКЛАД 1.

Знайти довжину дуги конічної гвинтової лінії     

від точки О(0;0;0;) до точки А

Розв’язок:

Знайдемо значення параметра  , яке відповідає положенню точки А.   тобто

 Знайдемо значення параметра  яке відповідає  положенню

точки О.   тобто  але ж . Звідси Це можливо лише при  

А тому

Підставимо  в  інтеграл ;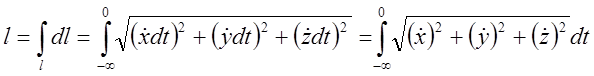

Обчислимо

;

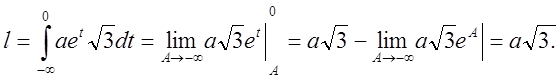
Відповідь:  

ПРИКЛАД 2.

 Обчислити 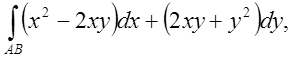де АВ – дуга параболи  від точки А(1;1) до точки В(2;4)

Розв’язок:

Підставимо в умову замість y те, чому він дорівнює коли ми проходимо вздовж кривої АВ, тобто . Ми одержимо звичайний одновимірний інтеграл з границями від  

до  

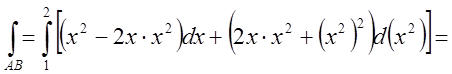
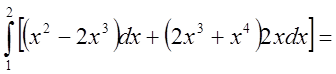
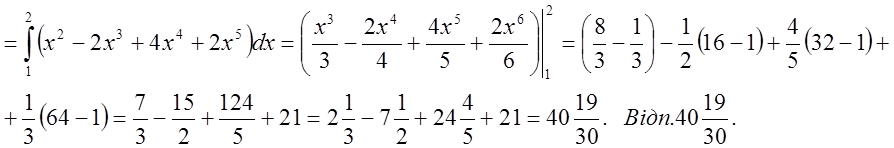
ПРИКЛАД 3.

Знайти момент інерції відносно осі z першого витка гвинтової лінії .

Розв’язок:

 Використаємо формулу , де r­­­­­ – відстань від маси  до осі l. Tак   як відстань до осі 0Z у гвинтової лінії постійна і  дорівнює ,то

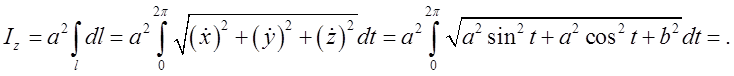
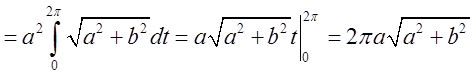. Це і є відповідь.

ПРИКЛАД 4.

Обчислити 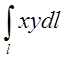, де l­- контур квадрата  

Розв’язок:

Запишемо рівняння сторін квадрата:

АВ:   x+y=a;    y=a-x;

BC:   y-x=a;     y=a+x;

CD:   x+y=-a;   y=-x-a;

AD:   x-y=a;      y=x-a;

Обчислимо ;

На AB y`=-1;     на BC  y`=1;    на СD   y`=-1;     на AD   y`=1.

Таким чином по всьому контуру  ;   

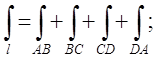
 Обчислимо окремо кожен з інтегралів.

;

  

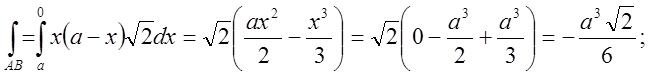
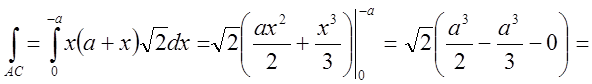
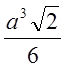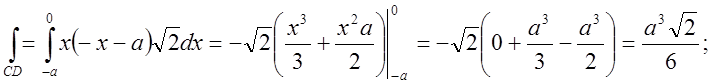
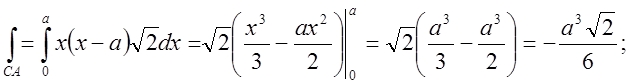
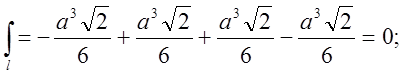
 Відповідь:  0.

ПРИКЛАД 5.

  Обчислити 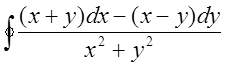, де контуром є коло, рух проти часової стрілки.

Розв’язок.

 Контуром візьмемо коло радіусом R. Тоді рівняння контура : , причому, для того щоб точка обійшла весь контур  повинно змінюватись від   до , а тому маємо  =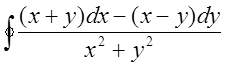

.

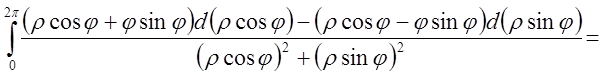
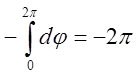 Це є відповідь.

Зауваження. Застосовувати формулу Гріна при розв’язувані цього прикладу ніяк не можна бо підінтегральні функції  P(x,y) i Q(x,y) в точці O(0,0), яка лежить в області D, мають розрив другого роду, а значить подвійний інтеграл буде невластивим. Перевіримо це.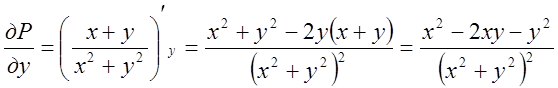         

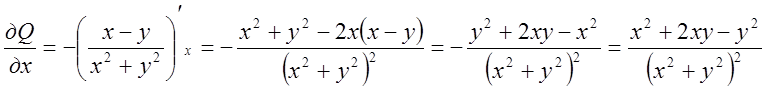. Підставимо

 =

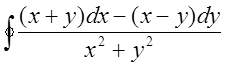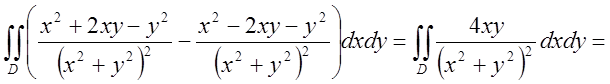
={якщо контуром є коло радіусом R, і ми переходимо в полярну систему координат, то границями для  будуть: , границями для  будуть: }=

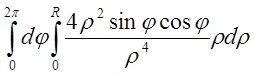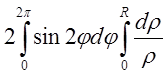==={внутрішній інтеграл дорівнює  і в нижній границі одержуємо }. Так, що застосовувати формулу Гріна можна лише при виконанні умов теореми.

3)  Розв’язати самомтійно:

1. 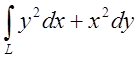, де контуром є верхня половина еліпса  x=a cost, y=b sint, рух по ходу годинної стрілки . Відп. .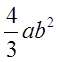

2.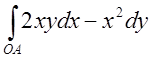 , узятий уздовж параболи, віссю симетрії якої є вісь ОУ від точки О(0,0) до точки А(2,1). Відп.0.

3. 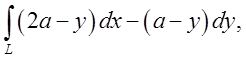де L – перша арка циклоїди . Відп..

4. Застосовуючи формулу Гріна, перетворити криволінійний інтеграл 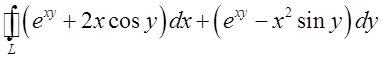, взятий по замкнутому контуру з додатнім напрямком обходу в подвійний інтеграл по області обмеженій цим контуром. Відп..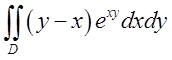   

Практичне заняття 11.

План:

11.1.Тема. Дослідження криволінійних інтегралів (продовження). Їх властивостей. Дослідження умови незалежності інтеграла від лінії інтегрування.Інтегрування повних диференціалів.

11.2.Ціль:

1). Засвоїти криволінійні інтеграли.

2). Засвоїти умови незалежності інтеграла від лінії інтегрування.

3). Засвоїти формулу Ньютона - Лейбніца.

11.3. Теоретичний матеріал подано в лекції номер 8.

11.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).

11.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 458-481.