Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 6

Тоді (5.10) перетворюється в 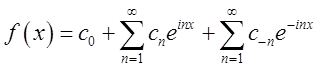  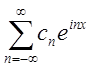  =(5.11)

Таким чином, ми одержали розвинення функції  у функціональний ряд з комплексними членами. Він називається  рядом Фур'є в комплексній формі.

 

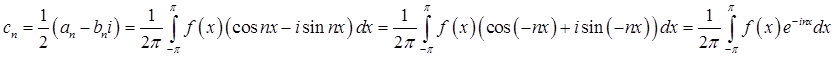
і аналогічно

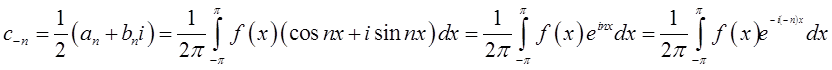
 Отже, при будь-якому цілому  , , ,…

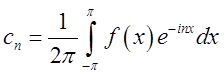                                                                     (5.12)

Якщо функція   дійсна ( а дотепер ми тільки такі функції і розглядали), то з формул (5.11) випливає, що коефіцієнти  розвинення в комплексний ряд Фур'є є комплексними спряженими числами. Для модулів цих чисел ми маємо

.

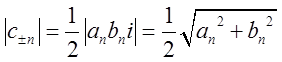Згадуючи інтерпретацію розкладання функції в тригонометричний ряд Фур'є як представлення руху у виді суми (суперпозиції) гармонійних коливань, ми бачимо, що модулі коефіцієнтів комплексного ряду Фур'є є амплітудами відповідних гармонік.

Безпосереднє розвинення функцій у комплексний ряд Фур'є на підставі формули (5.12) часто виявляється зручніше, ніж обчислення коефіцієнтів цього ряду через коефіцієнти дійсного ряду Фур'є по формулах (5.11).

5.7. Вправи на засвоєння матеріалу.

1).  Розв’яжемо декілька прикладів:

 ПРИКЛАД 1.

 Розвинути в ряд Фур’є функцію , де

Розв’язок:

             

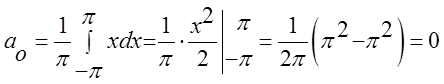
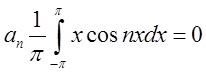
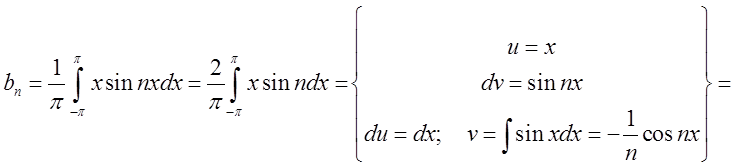
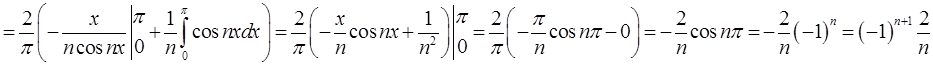
Підставимо в ряд  і отримаємо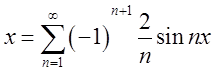

Відповідь:.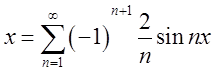

ПРИКЛАД  2.

 Розвинемо в ряд прямокутний імпульс заданий в інтервалі  так: 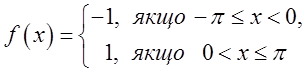 В точці х=0 імпульс переривається, тобто ця точка є точкою розриву функції.

Розв’язок:

Розв’язок. Так задана функція задовольняє умови теореми Діріхлє і оскільки вона непарна, то .

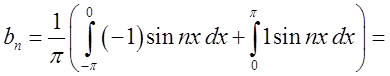
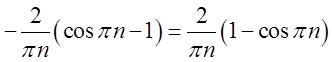. Так як  , то 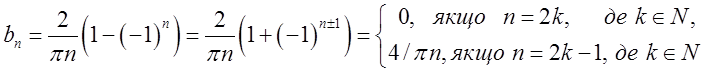 Підставимо знайдені коефіцієнти в (3.1), розвинення заданої функції в ряд Фур’є має вигляд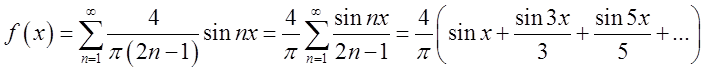

рис.3.1.

На цьому прикладі наглядно видно виконання  теореми Діріхлє. А й справді: при х=0 та  сума ряду 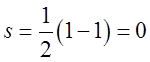. Використовуючи  рис.3.1, простежимо, яким чином графік функції імпульса наближено одержується з графіків послідовних частинних сум ряду Фур’є. На рис.3.1.а добре видно, що 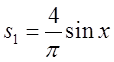 дорівнює 0 в точках  і віддалено наближує графік початкової функції в решті точок. Але наступна частиння сума 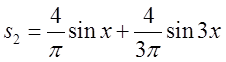,  на рис.3.1.б це суцільна крива лінія, яка по чотири рази перетинає кожен з відрізків імпульса, зберігаючи нульові значення в точках , вже набагато точніше  наближує графік початкової функції в решті точок.

ПРИКЛАД 3.

Рівень 4. Розвинемо в інтеграл Фур'є в комплексній формі функцію 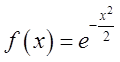( рис.3.7.)

Розв’язок:

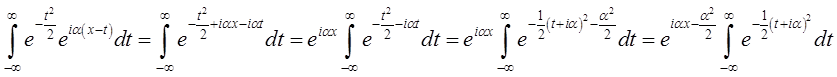 Останній інтеграл є функцією від a. Позначимо його через  і обчислимо його. Ми маємо       

 ,

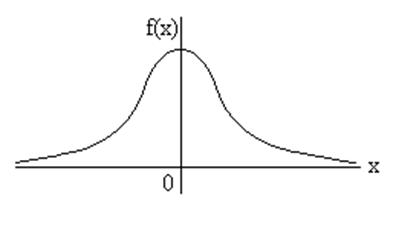
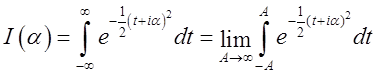роблячи підстановку , ми одержимо 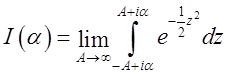. Продиференцюємо цю тотожність по a. Через те, що                                                                    збіжність до границі по a є рівномірною в будь-якому кінцевому проміжку, диференціювання під знаком границі законно. Ми маємо 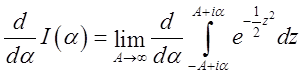. Виконуючи диференціювання інтегралу по верхній і нижній границях, ми одержуємо

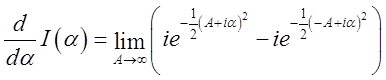 , а згадуючи формулу (3.23) і переходячи до границі, будемо мати 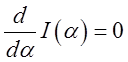. Отже, первісна функція повинна бути постійної:   . Зокрема, повинне бути . Обчислимо інтеграл . Запишемо його для цього двічі:

 , і перемножимо почленно ці рівності. Ми одержимо    .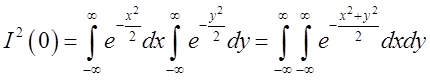

Переходячи в подвійному інтегралі до полярних координат, ми маємо

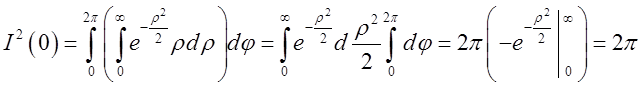 , відкіля . Таким чином,      і шуканим розвиненням в інтеграл Фур'є є 

      .

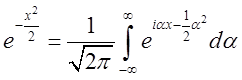Відповідь: .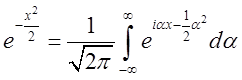

ПРИКЛАД 4.

Знайти розвинення в комплексний ряд Фур'є функції на сегменті .

Розв’язок:

 При кожнім ми тут маємо

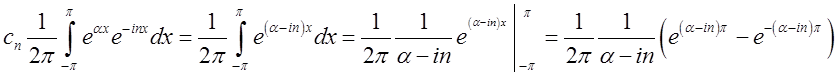
Зауважимо, що для будь-якого цілого  .

Тому       .

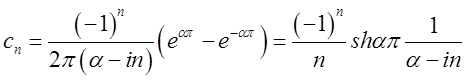Таким чином, шуканим розкладанням буде        .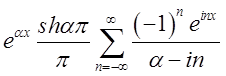

Відповідь: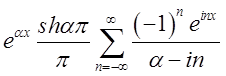   

Практичне заняття 6.

План:

6.1.Тема. Дослідження ортонормованих систем. Властивості коефіцієнтів Фур’є. Інтеграл Фур’є. Перетворення Фур’є, його властивості.

6.2.Ціль:

1). Засвоїти комплексну форму запису ряду Фур’є.

2). Засвоїти представлення функції інтегралом Фур’є.

3). Засвоїти комплексну форму інтегралу Фур’є.

4). Засвоїти поняття про перетворення Фур’є.

6.3. Теоретичний матеріал подано в лекції номер 3.