Введемо параметр t і вважаємо ![]() .
До цього нас штовхає не стільки наявність в першому рівнянні системи суми
.
До цього нас штовхає не стільки наявність в першому рівнянні системи суми ![]() , як те, що при такій параметризації в
другому рівнянні замість трьох змінних
, як те, що при такій параметризації в
другому рівнянні замість трьох змінних ![]() залишиться
тільки дві
залишиться
тільки дві ![]() . Після параметризації друге рівняння
перетвориться в рівняння з відокремленими змінними і легко інтегрується.
. Після параметризації друге рівняння
перетвориться в рівняння з відокремленими змінними і легко інтегрується. ![]() .
.
Таким чином параметричні рівняння векторних ліній будуть мати вид
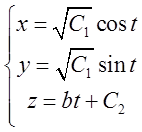 (*)
(*)
Знайдемо значення параметра t, яке відповідає точці ![]() ; при
; при ![]() маємо
маємо
![]() .
Підставимо це значення параметра а також координати точки в
.
Підставимо це значення параметра а також координати точки в ![]() в (*) і отримаємо:
в (*) і отримаємо:
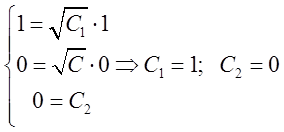 .
.
Тому параметричне рівняння векторної лінії яка проходить через точку ![]() буде гвинтова лінія
буде гвинтова лінія 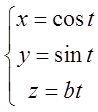 -
це і є відповідь.
-
це і є відповідь.
ПРИКЛАД 6.
Проводячи досліди з магнітним полем провідника струму при вивченні шкільного курсу фізики, ви спостерігали як залізні опилки під дією магнітного поля провідника перпендикулярного до площини, на якій розсипані опилки утворювали концентричні кола, центром яких є точка перетину вісі провідника з площиною. Знайдемо тепер рівняння векторних ліній магнітного поля нескінченного провідника, по якому тече струмом величиною І.
Розв’язок:
Систему координат виберемо так, щоб провідник співпав з напрямом вісі ![]() . Нехай струм має силу
. Нехай струм має силу ![]() ,
тоді для визначення вектора напруженості магнітного поля в точці
,
тоді для визначення вектора напруженості магнітного поля в точці ![]() , створюваного струмом, застосуємо закон
Біо-Савара у векторно-диференціальній формі
, створюваного струмом, застосуємо закон
Біо-Савара у векторно-диференціальній формі 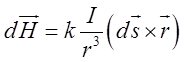 , де
, де ![]() – вектор напруги магнітного поля,
створеного струмом І, який проходить по дільниці-вектору
– вектор напруги магнітного поля,
створеного струмом І, який проходить по дільниці-вектору ![]() ;
; ![]() –
вектор, проведений з початку вектора
–
вектор, проведений з початку вектора ![]() в точку
в точку
![]() , в якій знаходимо напруженість.
, в якій знаходимо напруженість.
Позначимо зміну
віддаль між точкою О(0,0,0) і початком вектора ![]() через t. Тоді
через t. Тоді ![]() можна вважати як
приріст t, тобто,
якщо
можна вважати як
приріст t, тобто,
якщо ![]() , то
, то ![]() . Але ж
. Але ж
![]() і тому
і тому ![]() .
Очевидно, що
.
Очевидно, що ![]() ,
, ![]() . Якщо
. Якщо ![]() відстань від вісі Оz до точки
відстань від вісі Оz до точки ![]() , то
, то 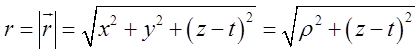 .
.
Розкриємо векторний добуток:
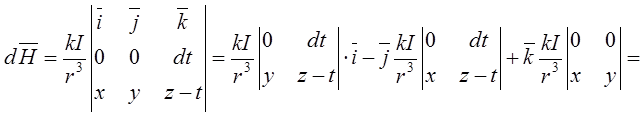
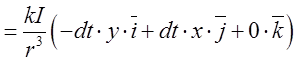 . Бачимо, що
. Бачимо, що 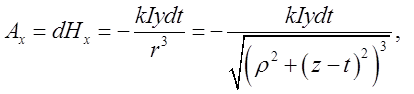
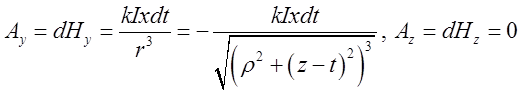 . Щоб знайти
. Щоб знайти ![]() проінтегруємо
знайдені диференціали в межах від
проінтегруємо
знайдені диференціали в межах від ![]() до
до ![]() .
.
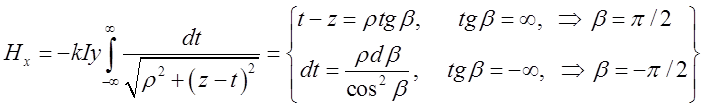 =
=
=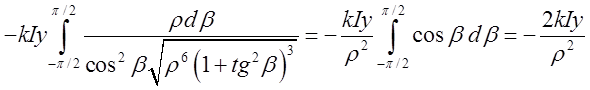 . Тобто
. Тобто 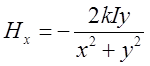 .
Аналогічно знайдемо
.
Аналогічно знайдемо 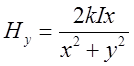 . З
. З ![]() .
.
Після скорочення
знаменників на 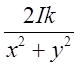 , диференціальні рівняння
векторних ліній будуть мати вигляд:
, диференціальні рівняння
векторних ліній будуть мати вигляд: 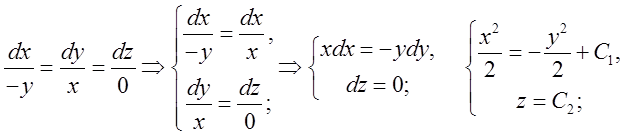
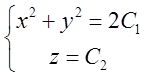 - це є рівняння сімейства кіл, центри яких
знаходяться на вісі Oz; радіуси цих кіл
- це є рівняння сімейства кіл, центри яких
знаходяться на вісі Oz; радіуси цих кіл ![]() і віддалені вони від площини
і віддалені вони від площини![]() на віддаль
на віддаль![]() .
.
ПРИКЛАД 7.
Обчислити потік вектора ![]() через
зовнішню сторону бічної поверхні кругового циліндра
через
зовнішню сторону бічної поверхні кругового циліндра ![]() ,
обмеженою площинами z=0 і z=H (H>0).
,
обмеженою площинами z=0 і z=H (H>0).
Розв’язок:
Даний циліндр проектуєтьсяна площину хОу
в лінію, а саме, в коло 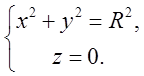
Тому будемо проектувати циліндр на інші координатні
площини, наприклад, на площину уОz. Тому що циліндр проектується на площину у0z
не взаємно однозначно, то скористаємося властивістю аддитивности потоку вектора
і представимо шуканий ноток К в виді суми потоків ![]() , де
, де ![]() — потік поля через частину
— потік поля через частину ![]() циліндра, розташовану в області, де у
> 0, а
циліндра, розташовану в області, де у
> 0, а ![]() — потік цього ж поля через
частину
— потік цього ж поля через
частину ![]() циліндра, розташовану в області, де у <
0. На
циліндра, розташовану в області, де у <
0. На ![]() маємо
маємо
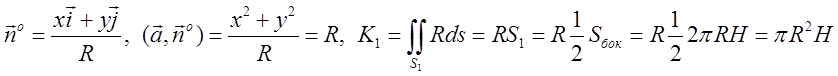 .
.
На поверхні S2 , аналогічно будемо мати

Загальний потік буде ![]() .
.
2)Розв’язати самостійного.
1.
Обчислити потік векторного поля ![]() через
верхню сторону трикутника, вирізаного з площини
через
верхню сторону трикутника, вирізаного з площини ![]() площинами
площинами![]() .Відп.
.Відп.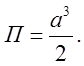
2. Обчислити потік векторного поля ![]() через зовнішню сторону параболоїда
через зовнішню сторону параболоїда ![]() обмеженого площиною
обмеженого площиною![]() .Відп.
.Відп.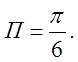
3. Обчислити
потік векторного поля ![]() через
бічну поверхню кругового циліндра
через
бічну поверхню кругового циліндра ![]() обмежену площинами
обмежену площинами ![]() . Відп.
. Відп.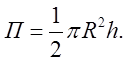
4. Обчислити потік векторного поля ![]() через верхню сторону кркга, що вирізується конусом
через верхню сторону кркга, що вирізується конусом ![]()
![]() на площині
на площині ![]() Відп.
Відп.![]()
5. Обчислити потік векторного поля ![]()
![]() через зовнішню сторону параболоїда
через зовнішню сторону параболоїда ![]() , розташовану в першому октанті. Відп.
, розташовану в першому октанті. Відп.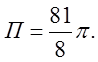
6. Обчислити
потік векторного поля![]()
![]()
через частину площини z=0, обмежену колом ![]() в напрямку орта
в напрямку орта ![]() .
Відп.
.
Відп.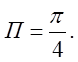
7. Обчислити потік векторного поля ![]() через повну поверхню конуса
через повну поверхню конуса ![]() ,
обмежену площиною
,
обмежену площиною ![]() . Відп.
. Відп.![]()
8. Обчислити потік векторного поля ![]() через замкнуту поверхню, обмежену параболоїдом
через замкнуту поверхню, обмежену параболоїдом ![]() і площиною z= 0. Відп.
і площиною z= 0. Відп.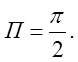
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.