Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 15

12.7. Вправи на засвоєння матеріалу.

1).  Розв’яжемо декілька прикладів:

 ПРИКЛАД 1.

Обчислити поверхневі інтеграли по площі поверхні (інтегрли І-го типу).

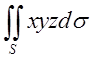, де S – частина площини , яка лежить в першому октанті

Розв’язок:

 Спроектувавши поверхню на площину хОу, застосуємо (10.7). Нормаль до площини утворює з віссю Oz гострий кут , , , а тому

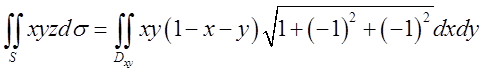 . Область  – частина площини  , обмежена  трикутником , а тому

                       Рис 10.4.      

=

     

=

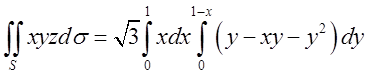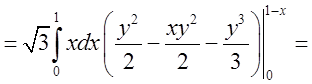
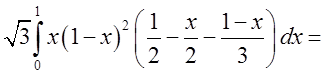
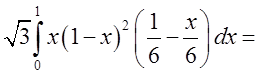
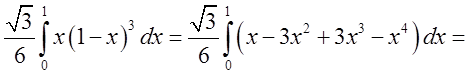
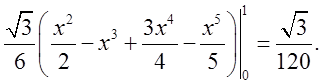
ПРИКЛАД 2.

Обчислити поверхневі інтеграли по площі поверхні (інтегрли І-го типу).

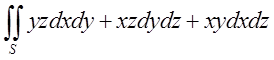 , де S – зовнішня сторона піраміди утвореної площинами .

Розв’язок:

Зовнішня сторона піраміди, див. рис.10.4, (як, до речі, і внутрішня) складається з чотирьох поверхонь її граней. Крім точки , вершинами піраміди будуть точки перетину площини  з вісями координат . Обчислення інтегралу заданого за умовою перетвориться в обчислення читирьох інтегралів по чотирьох частинах поверхні . Запишемо рівняння цих поверхонь і поведінку змінних та  їх диференціалів на цих поверхнях.

: рівняння ; змінюються всі змінні ;.

 : рівняння ; змінюються лише координати х і z. ; .

: рівняння ; змінюються лише координати х і  у. ; .

: рівняння ; змінюються лише координати z і  у. ; .

Обчислимо інтеграл по кожній з поверхонь.

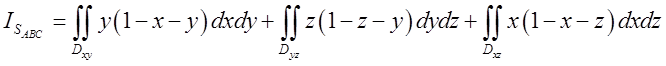. Зрозуміло за умовою на яку координатну площину який доданок проектується і яка змінна повинна виражатись через інші. Всі області мають однаковий вид – рівнобедрені прямокутні трикутники, а тому далі:

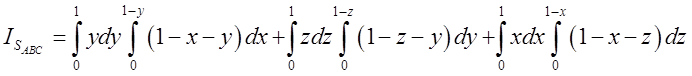. Інтеграли відрізняються один від одного лише видом змінних, тому за величиною вони однакові. Обчислимо перший.

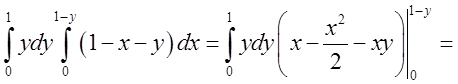
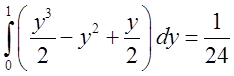.  буде втричі більший, тобто .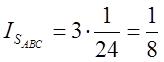

Приступимо до обчислення . Проектувати цю поверхню нікуди не треба бо вона вже лежить на координатній площині. ЇЇ проекції на інші координатні площини є відрізками ОА і ОВ, які не мають площі. Через те із трьох інтегралів 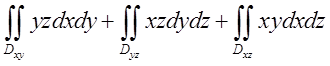два перших дорівнюють нулю із-за рівності нулю площі областей інтегрування, а третій при обчисленні також дасть нуль бо в цій області у=0.  По двох інших областях одержимо такий же результат і з тих же самих причин.

Відповідь. 1/8.

ПРИКЛАД 3.

 Обчислити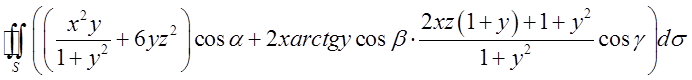 

 через замкнуту поверхню обмежену зверху  і знизу площиною .

Розв’язок:

 Застосуємо теорему Остроградського. Для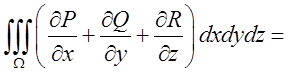

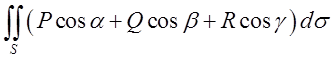
 обчислимо .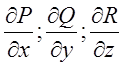

З виду інтеграла знаходимо: ;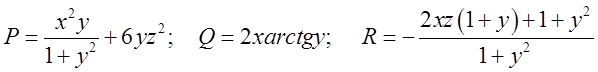

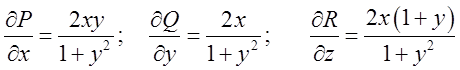.Обчислимо ;

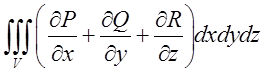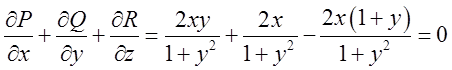. А це значить, що .

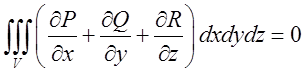Відповідь: 0

ПРИКЛАД 4.

Обчислити криволінійний інтеграл 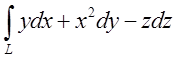, де  - контур .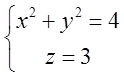

Розв’язок:

Застосуємо теорему Стокса і формулу 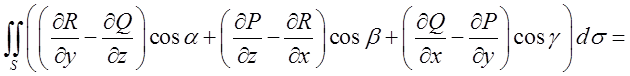 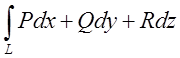      Для цього на коло 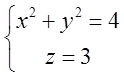, “натягнемо” яку – небудь поверхню. Звичайно візьмемо найпростішу – круг. Поверхня буде мати вигляд: 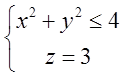. Для застосування теореми Стокса обчислимо 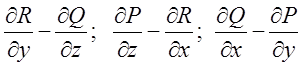, де

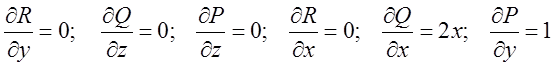. Тому перші дві різниці дорівнюють 0,

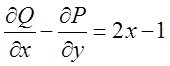. Підставляючи в формулу Стокса одержимо: 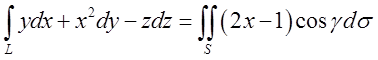, де S – поверхня 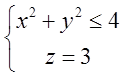. Так як S паралельна площиніто  і  , як відомо  і поверхневий інтеграл дуже легко зводиться до подвійного 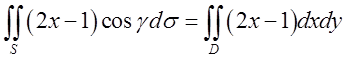 - де  - круг , який лежить на площині . Перейдемо до полярної системи координат

, границі очевидні .

=

.

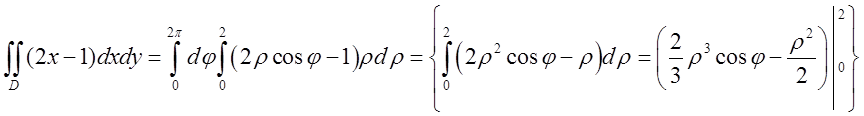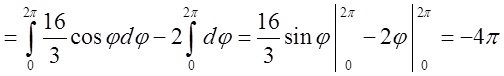 Відповідь: .

2) Розв’язати сомостійно:   

10.1. Обчислити поверхневі інтеграли першого типу:

а)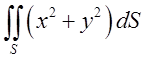, де S – сфера . Відп. .

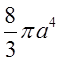б) 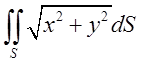, де S – бокова поверхня конуса .

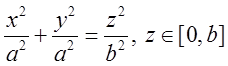Відп..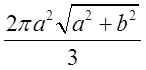

10.2. Обчислити 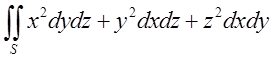, де S – зовнішня сторона поверхні напівсфери

.   Відп. .

Практичне заняття 13.

План:

13.1.Тема. Дослідження теорії поля. Поняття градієнта. Векторне поле і векторні лінії. Дослідженняпотока вектора через поверхю.

13.2.Ціль:

1). Засвоїти скалярне поле.

2). Засвоїти означення градієнта.

3). Засвоїти векторне поле і векторні лінії.

13.3. Теоретичний матеріал подано в лекції номер 11.

13.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).

13.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 491-505.