13.6. На практичному занятті використовуються формули, таблиці, теореми.
1). Скалярне поле. Поверхні рівня.
Означення.
Якщо в області D задана скалярна функція точки ![]() , то говорять, що в цій області задане скалярне
поле.
, то говорять, що в цій області задане скалярне
поле.
Ми
будемо вважати, що скалярне поле стаціонарне, т, е. що величина ![]() не залежить від часу t. Зауважимо,
втім, що в реальному оточені приходиться
зіштовхуватися і з нестаціонарними полями. Тоді величина
не залежить від часу t. Зауважимо,
втім, що в реальному оточені приходиться
зіштовхуватися і з нестаціонарними полями. Тоді величина ![]() буде залежати не тільки від точки Р, але і від часу t
буде залежати не тільки від точки Р, але і від часу t![]() .
.
Означення. Поверхнею
рівня скалярного поля
називається геометричне місце точок, у яких функція ![]() приймає постійне значення, тобто
приймає постійне значення, тобто ![]() .
.
Означення. Похідною від функції ![]() у напрямку
у напрямку ![]() в точці Р називається границя (якщо вона існує)
в точці Р називається границя (якщо вона існує) 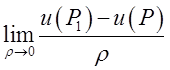 =
=
=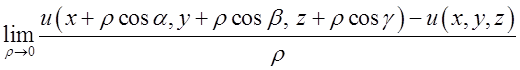 .
.
2) Градієнт.
Означення. Градієнтом функції ![]() називається вектор,
проекціями якого служать значення частинних похідних цієї функції,
тобто
називається вектор,
проекціями якого служать значення частинних похідних цієї функції,
тобто
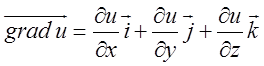
Похідна функції по напрямку дорівнює скалярному добутку градієнта функції на одиничний вектор цього напрямку.
З перетворення 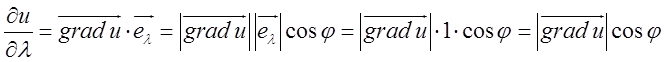 , ми
бачимо що похідна функції
по даному напрямку дорівнює проекції градієнта функції на напрямок
диференціювання, де
, ми
бачимо що похідна функції
по даному напрямку дорівнює проекції градієнта функції на напрямок
диференціювання, де ![]() -кут між вектором
-кут між вектором ![]() і променем
і променем ![]() .
.
Властивості градієнта функції аналогічні правилам знаходження похідних і доведення двох наступних властивостей очевидне.
1)![]() .
.
2)![]() , де С – постійна величина.
, де С – постійна величина.
Третю і четверту властивість доводимо за правилами диференціювання.
3)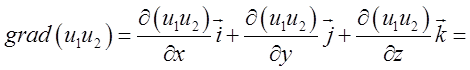
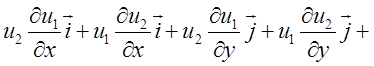
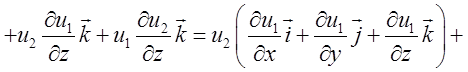
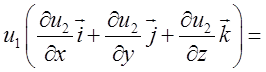
= ![]() . Таким чином:
. Таким чином: ![]()
![]() .
.
4) 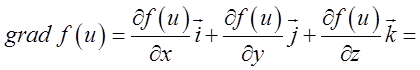
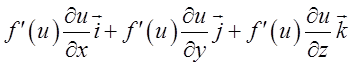 =
=
=![]() . Таким чином.
. Таким чином. ![]()
![]() .
.
3) Векторне поле і векторні лінії.
Означення. Якщо в кожній точці Р області D задано визначений вектор, то будемо говорити, що в цій області задане векторне поле.
Означення. Векторною лінією векторного поля називається лінія, у кожній точці якої напрям дотичної збігається з напрямком вектора, що відповідає цій тічці.
13.7. Вправи на засвоєння матеріалу.
1). Розв’яжемо декілька прикладів:
ПРИКЛАД 1.
Знайти поверхні рівня скалярного
поля 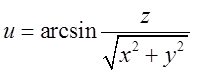 .
.
Розв’язок.
Знайдемо спочатку область визначення функції:
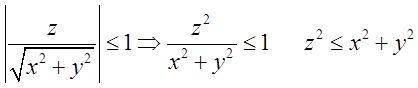 ; як відомо
; як відомо ![]() є рівняння конуса. Значить нерівність
є рівняння конуса. Значить нерівність ![]() задає
простір який знаходиться зовні конуса. Для цього достатньо взяти яку завгодно
точку, про яку ми знаємо, що вона знаходиться зовні, наприклад
задає
простір який знаходиться зовні конуса. Для цього достатньо взяти яку завгодно
точку, про яку ми знаємо, що вона знаходиться зовні, наприклад ![]() і переконатись, що її координати задовольняють
нерівність
і переконатись, що її координати задовольняють
нерівність ![]() . Поверхні рівня визначаються рівнянням
. Поверхні рівня визначаються рівнянням 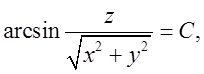 де
де 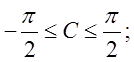 Або
після очевидних перетворень
Або
після очевидних перетворень 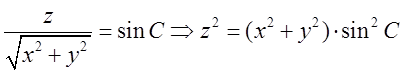 . Але ж
. Але ж ![]() тому
тому ![]() - це буде сімейство кругових
конусів розташованих зовні конуса
- це буде сімейство кругових
конусів розташованих зовні конуса ![]() зі спільною віссю симетрії
зі спільною віссю симетрії ![]() . Сам конус
. Сам конус ![]() також
входить в це сімейство, а точка
також
входить в це сімейство, а точка ![]() - вершина всіх конусів є точкою невизначеності поля.
- вершина всіх конусів є точкою невизначеності поля.
ПРИКЛАД 2.
Знайти похідну
скалярного поля ![]() в точці
в точці![]() параболи
параболи![]() за напрямком цієї параболи.
за напрямком цієї параболи.
Розв’язок.
Знайдемо направляючі конуси вказаного напрямку. Напрям параболи, в
будь-якій точці збігається з напрямком дотичної до параболи в цій точці, а тому
знайдемо вектор напрямку (добре було б, коли б він був одиничним) дотичної,
використовуючи геометричний зміст похідної: тангенс кута нахилу до осі ![]() дотичної до кривої в даній точці дорівнює величині
похідної в цій точці. Із рівняння
дотичної до кривої в даній точці дорівнює величині
похідної в цій точці. Із рівняння 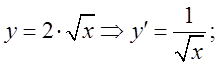 Тому
Тому
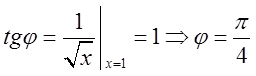 ; Звідси
; Звідси 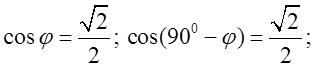
Таким чином 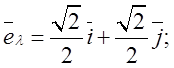 Знайдемо
Знайдемо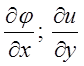 в точці
в точці ![]()
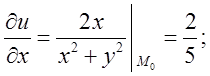
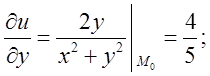 Підставимо знайдені значення в формулу (11.1).
Підставимо знайдені значення в формулу (11.1).
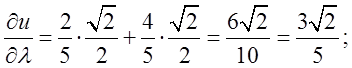
Це і є відповідь.
ПРИКЛАД 3.
Обчислити ![]() , де
, де 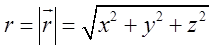 –
довжина радіус-вектра
–
довжина радіус-вектра ![]() точки
точки ![]() ,
або віддаль цієї точки від початку координат.
,
або віддаль цієї точки від початку координат.
Розв’язок:
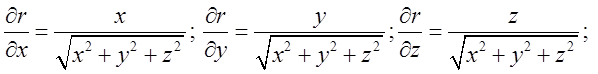 Очевидно, що
Очевидно, що 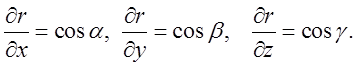 А
тому
А
тому ![]() .
.
ПРИКЛАД 4.
Знайти точки, в яких
модуль градієнта скалярного поля ![]() дорівнює
1.
дорівнює
1.
Розв’язок:
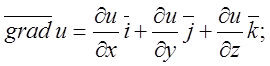
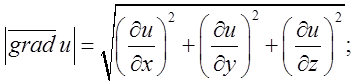 (*)
(*)
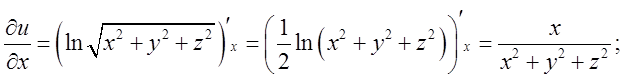
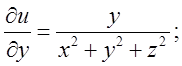
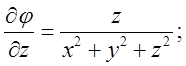 Підставимо в (*)
Підставимо в (*) 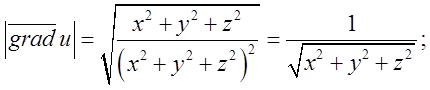 Згідно
умови
Згідно
умови ![]() , тобто
, тобто ![]() ,
а це рівняння сфери.
,
а це рівняння сфери.
Відповідь: точки
розміщені на сфері ![]() .
.
ПРИКЛАД 5.
Знайти векторну
лінію поля![]() , яка проходить через точку
, яка проходить через точку ![]() ; .
; .
Розв’язок:
Скористаємось для
знаходження векторних ліній диференційними рівняннями 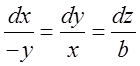 ; це система рівнянь. Представимо її у вигляді:
; це система рівнянь. Представимо її у вигляді:
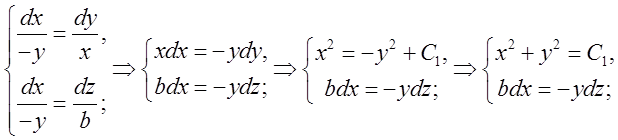 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.