4.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 670-691.
4.6. На практичному занятті використовуються формули, таблиці, теореми.
1). Означення рядів Тейлора та Маклорена.
Ряд 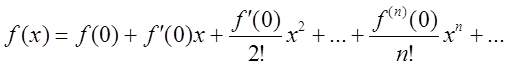
називається рядом Тейлора
для ![]() .
.
Справедлива така теорема.
Т. Ряд Тейлора (Маклорена) для ![]() збігається саме до
збігається саме до ![]() ,
якщо існує
,
якщо існує ![]() таке, що
таке, що
![]()
у деякому околі точки ![]()
2) Стандартні розвинення елементарних функцій в степеневі ряди.
Виконаємо розвинення деяких елементарних функцій у ряди Маклорена.
1.
Нехай ![]() . Маємо
. Маємо![]() ,
, ![]() ,
, ![]() ,…,
,…,![]() ,…, а
тому
,…, а
тому
![]()
![]()
![]() …=
…=![]()
Згідно з (4.2) ![]() =
=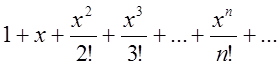 (4.1)
(4.1)
Знайдемо інтервал збіжності
цього ряду. За ознакою Даламбера 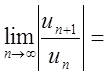
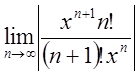 =
=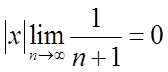 . Яке б не було х остання рівність завжди
виконується, а тому
. Яке б не було х остання рівність завжди
виконується, а тому ![]() .
.
2.
Нехай ![]() .
Тоді
.
Тоді ![]() ,
, ![]() ,
, ![]() ,
,![]() , …,
, …,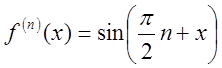 ,… При х = 0 дістанемо
,… При х = 0 дістанемо ![]()
![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]() … Підставивши в (4.2) одержимо
… Підставивши в (4.2) одержимо ![]() =
=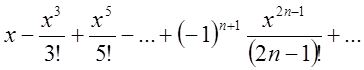 (4.6)
(4.6)
3.
Нехай ![]() .
Тоді
.
Тоді ![]() ,
, ![]() ,
, ![]() ,
,![]() , …,
, …,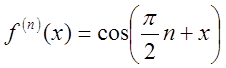 ,… При х = 0 дістанемо
,… При х = 0 дістанемо ![]()
![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]() … Підставивши в (4.2) одержимо
… Підставивши в (4.2) одержимо ![]() =
=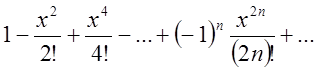 (4.7)
(4.7)
4.
Нехай маємо ![]() . Послідовно знайдемо похідні
. Послідовно знайдемо похідні
![]()
![]()
![]()
![]()
![]()
![]()
…………………………………. …………………………
![]()
![]()
………………………………………………. …………………………………….
Ураховуючи, що ![]() , після підстановки знайдених коефіцієнтів
в (4.2) одержимо
, після підстановки знайдених коефіцієнтів
в (4.2) одержимо 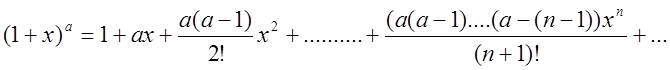 (4.8)
(4.8)
Ряд (4.8) називається біномінальним.
3). Формули Єйлера.
![]()
![]()
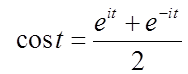
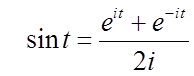
Дані формули називаються формулами Ейлера. Вони виражають тригонометричні функції через показникові і навпаки.
3). Застосування степенневих рядів:
4.7. Вправи на засвоєння матеріалу.
1). Розв’яжемо декілька прикладів:
ПРИКЛАД 1.
Розвинути в ряд за степенями x функцію ![]() .
.
Розв’язання:
Спочатку треба знайти значення функції та її похідних при x=0:
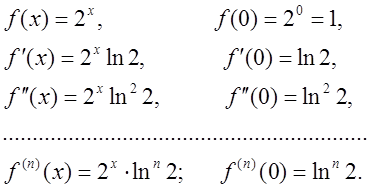
![]() тому при фіксованому x має місце нерівність
тому при фіксованому x має місце нерівність ![]() для всіх n.
для всіх n.
Функція можна представити у формі суми ряду Маклорена:
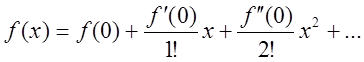 у даному випадку питання про збіжність ряду вирішується
ознакою Даламбера.
у даному випадку питання про збіжність ряду вирішується
ознакою Даламбера.
Відповідь: 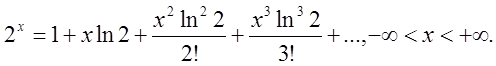
ПРИКЛАД 2.
Скласти для функції 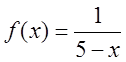 ряд Тейлора за степенями x-2.
ряд Тейлора за степенями x-2.
Розв’язання:
Треба обчислити значення функції f(x) та її послідовні похідні при x=2:
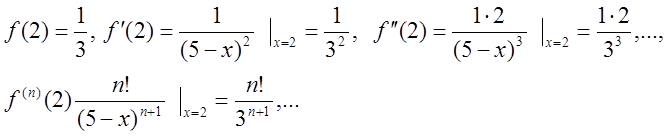 область збіжності одержаного ряду визначемо за допомогою
Р.П.К.
область збіжності одержаного ряду визначемо за допомогою
Р.П.К. 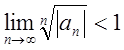 .
.
Зведемо тотожними перетвореннями
задану функцію 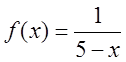 до формули суми
до формули суми ![]() - спадної геометричної прогресії
- спадної геометричної прогресії 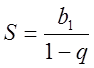 , звідки
, звідки ![]()
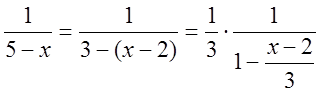 , звідси видно, що
, звідси видно, що 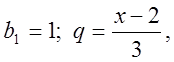 тому
тому 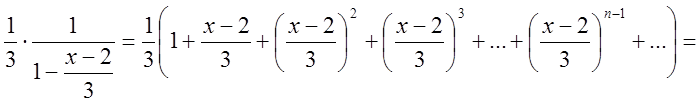
=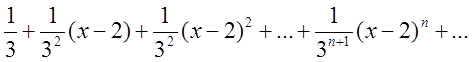
Відповідь: 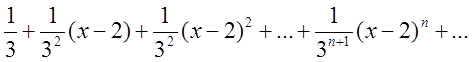
ПРИКЛАД 3.
Використовуючи стандартні розвинення
в ряди, розкласти за степенями х функцію 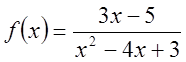 .
.
Розв’язання:
Представимо функцію ![]() у вигляді суми двох функцій. Таке представлення можливе бо знаменник
дробу можна записати у вигляді добутку двох двочленів
у вигляді суми двох функцій. Таке представлення можливе бо знаменник
дробу можна записати у вигляді добутку двох двочленів
![]() і потім, застосувавши метод невизначених коефіцієнтів прийдемо до суми.
і потім, застосувавши метод невизначених коефіцієнтів прийдемо до суми. 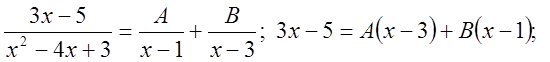 перегрупуємо
перегрупуємо
![]() . Для знаходження невизначених коефіцієнтів А і В одержуємо систему
. Для знаходження невизначених коефіцієнтів А і В одержуємо систему 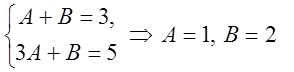 . Таким чином
. Таким чином 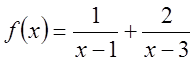 . Перетворимо ці доданки так, щоб можна було
застосувати до кожного з них формулу суми нескінченно спадної геометричної
прогресії.
. Перетворимо ці доданки так, щоб можна було
застосувати до кожного з них формулу суми нескінченно спадної геометричної
прогресії. 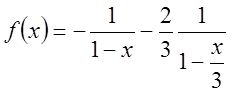 =
=![]()
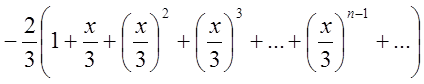 ={область збіжності першого ряду
={область збіжності першого ряду ![]() , другого
, другого ![]() . Зрозуміло, що область збіжності суми буде
. Зрозуміло, що область збіжності суми буде ![]() }=
}=
=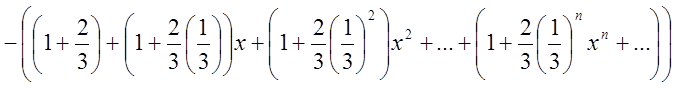 =
=
=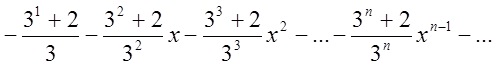
Відповідь: 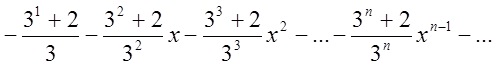
ПРИКЛАД 4.
Обчислити ![]() з точністю до 0,0001.
з точністю до 0,0001.
Розв’язання:
Треба скористатися розкладенням ![]() в ряд, x=0,1, m=1/5.
в ряд, x=0,1, m=1/5.
Маємо 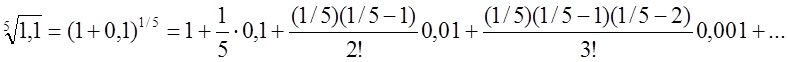
![]()
четвертий та інші після нього члени відкидаємо, тому що вони менші ніж 0,0001, ізгідно зтеоремою Лейбніца не впливають на зміну точності.
Відповідь: ![]()
![]() .
.
ПРИКЛАД 5.
Розв’язання:
Віднімемо від першої формули (4.12)
другу 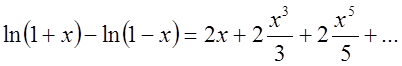
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.