Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 11

9.3. Теоретичний матеріал подано в лекції номер 6.

9.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).

9.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 4429-440.

9.6. На практичному занятті використовуються формули, таблиці, теореми.

          1). Застосування кратного інтегралу.

1.Площа плоскої фігури S: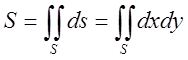                                      

1а. Площа поверхні , однозначна проекція, якої на площину хОу є D

                                                                      

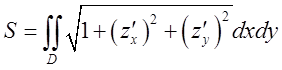
2.Обєм фігури V обмеженої циліндричною поверхнею і поверхнями: зверху ; знизу , D – область-проекція фігури V на площину ХОУ.

                               

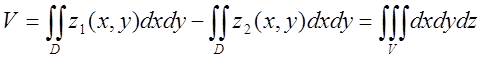
3.Маса плоскої пластинки змінної  густини .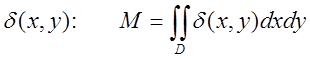

4. Маса обємного тіла V змінної  густини :

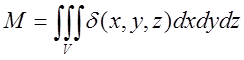
5.Статичні моменти пластинки: ,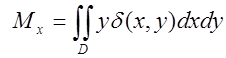

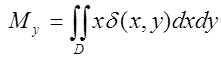
6.Статичні моменти відносно координатних  площин неоднорідного тіла, яке  займає об’єм V:   ; ;  .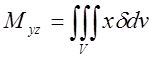

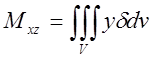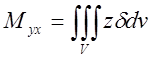7.Координати центру ваги пластинки: ;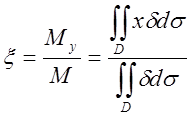

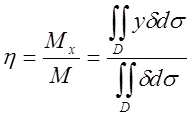
8.Координати центра ваги  неоднорідного тіла, яке займає в просторі об'єм V: ;:.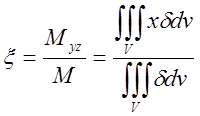                    

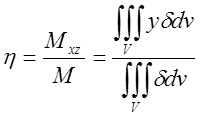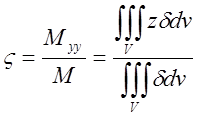9. Моментом інерції матеріальної точки Р з масою m відносно якої-небудь осі називається добуток  маси на квадрат віддалі точки Р до цієї осі.

Моменти  інерції пластинки із  змінною густиною  відносно координатних осей.

                                      

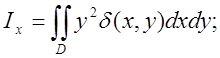
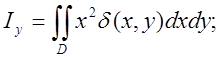
10. Аналогічно обчислюються моменти інерції відносно осей неоднорідного тіла з густиною , яке займає обєм V:

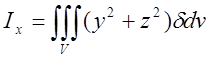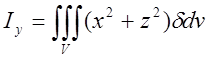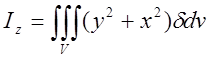; ;.                           (6.10)                      11.Відцентровий момент інерції: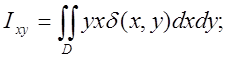                                   

11. Полярний момент інерції:

;                              

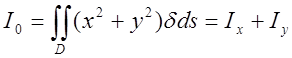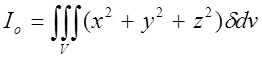
9.7. Вправи на засвоєння матеріалу.

1).  Розв’яжемо декілька прикладів:

 ПРИКЛАД 1.

Знайти момент інерції  еліптичного однорідного кільця, утвореного двома еліпсами з спільним центром і співпадаючими осями (“концентричні” еліпси). Осі зовнішнього еліпса  см. і  см.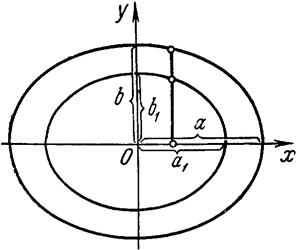

Розв’язок:

Обчислимо моменти інерції чверті еліптичного кільця, розташованого в першій чверті. Для цього обчислимо моменти інерції  та  площі, обмеженої зовнішнім еліпсом та осями координат , та віднімемо від них відповідно моменти інерції  і  площі, обмеженої внутрішнім еліпсом та осями координат.

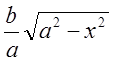В першій чверті на площі, обмеженій зовнішнім еліпсом та осями координат, змінні  та  міняються в таких межах:  від 0 до ;  від 0 до .

Тому      .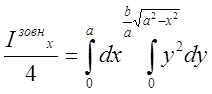

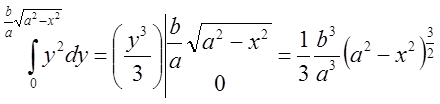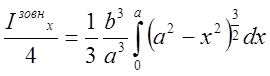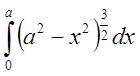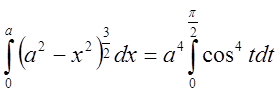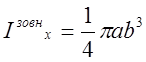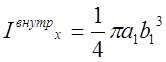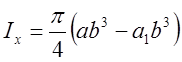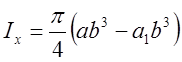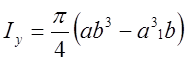Внутрішній інтеграл . Тому . Для обчислення  зручно застосувати тригонометричну підстановку: . Границі інтегрування після підстановки будуть дорівнювати 0 і , а . В результаті обчислень виявиться, що  см⁴. Досконало зрозуміло, що . Тому  см⁴ і остаточно момент інерції еліптичного концентричного кільця відносно осі   см⁴, відносно осі  –  см⁴.

ПРИКЛАД 2.

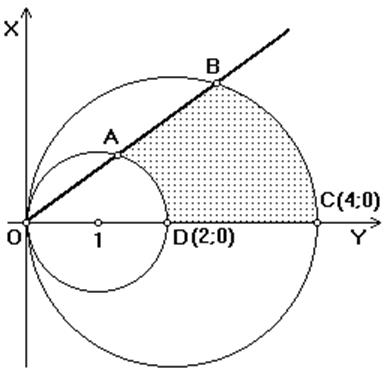 Знайти площу фігури, обмежену лініями

             x²+y²=2x, x²+y²=4x, y=x, y=0.

Розв’язок:

Площа фігури знаходиться за формулою 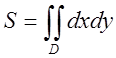. Зобразимо фігуру D обмежену заданими кривими, площу якої S треба знайти, рис. 6.1. Для цього спростимо задані рівняння кривих, якими вона обмежена:                                                    Рис. 9.1.                 

В перших двох рівняннях виділимо повні квадрати (x-1)²+y²=1 і  (x-2)²+y²=4. Ці два кола разом з прямими  y=0  і y=x  утворюють фігуру ABCD, площу якої і треба знайти. При                                          розв`язанні доцільно перейти до полярної системи координат. Ця доцільність випливає з того, що область обмежена двома променями y=0  і y=x  (в полярній системі це будуть 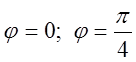 і це межі інтегрування зовнішнього інтеграла), а також із наявності в рівняннях кривих  x²+y². При переході в полярну систему координат цей вираз перетвориться в . Отож, перейдемо до полярної системи координат: x=rcos jy=rsin j.   Підставляємо ці значення x і y в початкові рівняння кривих: