Знакододатнім рядом називається ряд, в якому ![]() .
Згідно з теоремою 2, 1.2, немає необхідності окремо розглядати випадки знаковід’ємних рядів.
.
Згідно з теоремою 2, 1.2, немає необхідності окремо розглядати випадки знаковід’ємних рядів.
Нагадаємо один результат з теорії границь: монотонно зростаюча й обмежена зверху послідовність має границю.
2). Ознаки збіжності знакододатніх рядів.
Ознаки порівняння (О – П)
Т.1. Нехай маємо ряди![]() , (*)
, (*) ![]() ,(**)
,(**)
причому ![]() . Тоді із збіжності ряду (**) випливає збіжність ряду (*), а
з розбіжності ряду (*) випливає розбіжність ряду (**).
. Тоді із збіжності ряду (**) випливає збіжність ряду (*), а
з розбіжності ряду (*) випливає розбіжність ряду (**).
Т.2. Нехай маємо ряди ![]() , (*)
, (*)
![]() , (**)
, (**)
Якщо 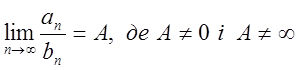 то ряд (*) і ряд (**)
мають однакову поведінку тобто вони одночасно розбігаються, або одночасно
збігаються..
то ряд (*) і ряд (**)
мають однакову поведінку тобто вони одночасно розбігаються, або одночасно
збігаються..
Ознака д’Аламбера (О –Д).
Т. Якщо![]() -загальний член ряду і
-загальний член ряду і 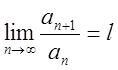 (1.2)
(1.2)
То а) при ![]() ряд
збіжний, б) при
ряд
збіжний, б) при ![]() ряд розбіжний,
ряд розбіжний,
в) при ![]() ознака не чинна:
існують ряди збіжні, для яких
ознака не чинна:
існують ряди збіжні, для яких ![]() і розбіжні, для яких
теж
і розбіжні, для яких
теж ![]() .
.
Радикальна ознака Коші (Р – К)
Т. Якщо![]() – загальний член ряду і
– загальний член ряду і
![]()
то а) при ![]() ряд
збіжний, б) при
ряд
збіжний, б) при ![]() ряд розбіжний,
ряд розбіжний,
в) при ![]() ознака не чинна:
існують ряди збіжні, для яких
ознака не чинна:
існують ряди збіжні, для яких ![]() і розбіжні, для яких
теж
і розбіжні, для яких
теж ![]() .
.
Інтегральна ознака Коші-Маклорена (І – К)
Т. Якщо члени ряду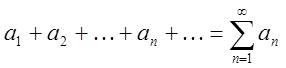 , (3.2)
, (3.2)
утворюють
незростаючу послідовність ![]() й існує незростаюча
неперервна невід’ємна функція
й існує незростаюча
неперервна невід’ємна функція ![]() така, що
така, що
![]() ,
, ![]() ,…,
,…, ![]() ,…,
,…,
то ряд (3) і
невластивий інтеграл 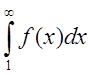 збігаються або розбігаються
одночасно.
збігаються або розбігаються
одночасно.
3). Лейбніцева ознака збіжності знакозмінних рядів.
О. Знакопереміжним називається ряд
![]() ,
, ![]() для
всіх
для
всіх ![]() . (4.2)
. (4.2)
Ознаку збіжності таких рядів містить наступна теорема.
Т. (Лейбніца). Якщо послідовність членів ряду (4.2)
1)
є спадною (![]() ),
),
2)
такою, що ![]() , то
, то
а) ряд (4.2) збігається,
б) якщо ![]() - сума ряду (4.2), то
- сума ряду (4.2), то ![]() .
.
Зауваження. Теорема Лейбніца справджується, якщо послідовність членів (4.2) є спадною хоча б з деякого номера.
2.7. Вправи на засвоєння матеріалу
1). Розв’яжемо декілька прикладів:
ПРИКЛАД 1.
Дослідити на збіжність ряд 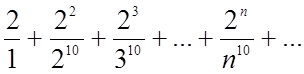
Розвязання:
Скористатися ознакою Даламбера (1.2).
Маємо ![]()
D=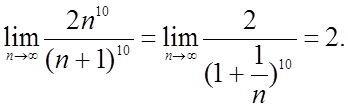
D>1, ряд розбіжний.
Відповідь: ряд розбіжний.
ПРИКЛАД 2.
Дослідити на збіжність ряд 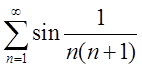 .
.
Розв’язання.
Маємо 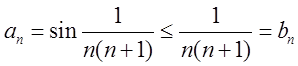 ,
, 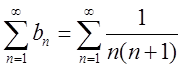 .
.
Останній ряд збіжний див (О-П), а тому за теоремою порівняння (Т-1) досліджуваний ряд збігається.
Відповідь: ряд збіжний.
ПРИКЛАД 3.
Дослідити на збіжність ряд 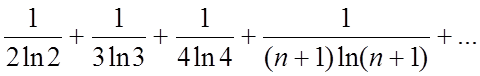
Розв’язання:
Скористатися інтегральною ознакою:
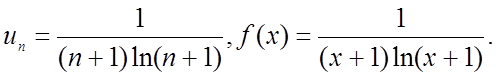
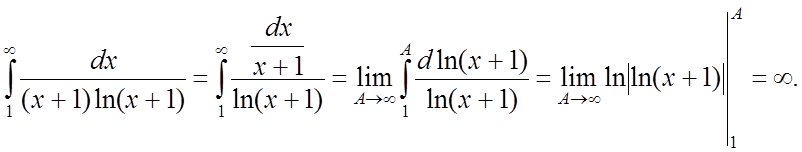
Інтеграл розбіжний, тому розбіжний і ряд.
Відповідь: ряд розбіжний.
ПРИКЛАД 4.
Дослідити на збіжність ряд 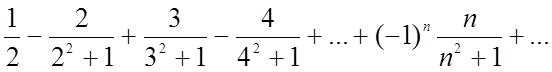
Розвязання:
Скористатися ознакою Лейбніца: 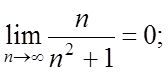
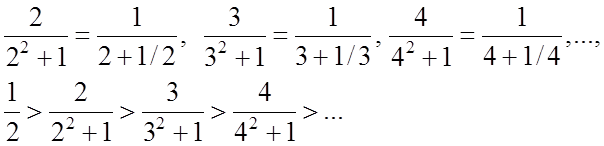
перша умова ознаки Лейбніца виконана.
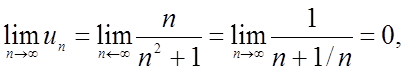 друга умова ознаки Лейбніца теж виконана.
друга умова ознаки Лейбніца теж виконана.
Значить ряд збіжний.
Відповідь: ряд збіжний.
ПРИКЛАД 5.
Дослідити на збіжність ряд 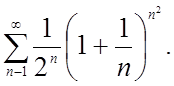
Розв’язання:
Скористатися радикальною ознакою Коши (І-К) :
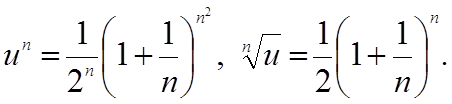
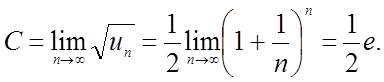 С>1, ряд розбіжний.
С>1, ряд розбіжний.
Відповідь: ряд розбіжний.
2). Розв’язати самостійно:
1. Дослідити збіжність рядів, використовуючи радикальну ознаку Коші.
1.1.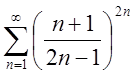 1.2.
1.2.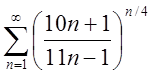 1.3.
1.3.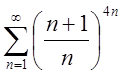 1.4.
1.4.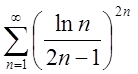
Від.1,2 – збіг.3,4 – розбіг
2. Дослідити збіжність рядів, використовуючи інтегральну ознаку Коші.
2.1. 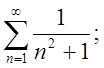 2.2.
2.2. 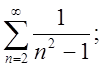 2.3.
2.3. 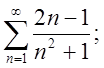 2.4.
2.4. 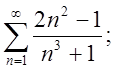
Відп.1,2 – збіг.3,4 – розбіг.
3. Дослідити збіжність знакозмінних рядів, використовуючи ознаку Лейбніца.
3.1. 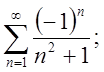 3.2.
3.2. 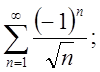 3.3.
3.3. 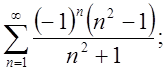 3.4.
3.4. 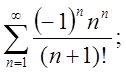
Відп.1-збіг. абсолютно, 2 – збіг. умовно, 3 і 4 – розбігаються.
Практичне заняття 3.
План:
3.1.Тема. Дослідження на збіжність функціональних рядів, властивостей рівномірнозбіжних рядів. Розвинення степенневих рядів. Абелева теорема.
3.2.Ціль:
1). Засвоїти функціональні ряди.
2). Засвоїти властивості рівномірнозбіжних рядів.
3). Засвоїти теорему Абеля.
3.3. Теоретичний матеріал подано в лекції номер 2.
3.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.