7.2.Ціль:
1). Засвоїти подвійні інтеграли, їх властивості.
2). Засвоїти обчислення в декартових координатах
3). Засвоїти заміну змінних у подвійних інтегралах.
7.3. Теоретичний матеріал подано в лекції номер 4.
7.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).
7.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 420-429.
7.6. На практичному занятті використовуються формули, таблиці, теореми.
1). Обчислення подвійного інтегралу.
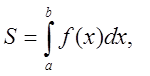
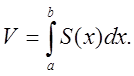 (пригадаймо матеріал ІІ-го семестру)
(пригадаймо матеріал ІІ-го семестру)
![]()
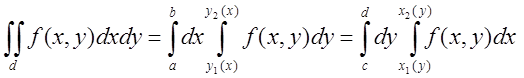
2). Заміна змінних у подвійному інтегралі.
Нагадаємо схему заміни змінних у визначеному
інтеґралі 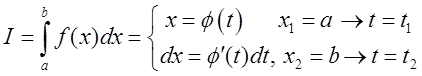
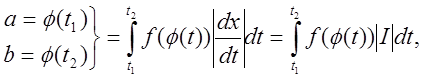
де
![]() — відношення довжин елементарних частин
при старій та новій змінних. Нехай маємо
— відношення довжин елементарних частин
при старій та новій змінних. Нехай маємо 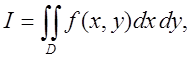
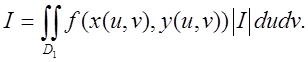
Користуючись
формулою Тейлора для двох змінних
(пригадаємо її: 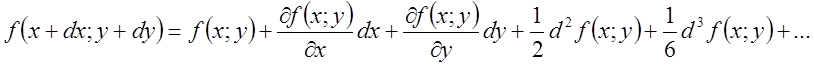 ),
),
маємо
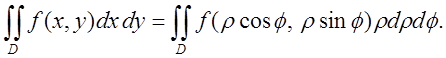 Формула є
формулою переходу в подвійному інтегралі від прямокутних декартових координат
до полярних.
Формула є
формулою переходу в подвійному інтегралі від прямокутних декартових координат
до полярних.
7.7. Вправи на засвоєння матеріалу.
1). Розв’яжемо декілька прикладів:
ПРИКЛАД 1.
Обчислити повторний інтеграл
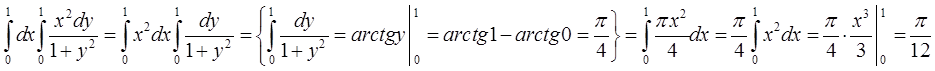 Відповідь:
Відповідь:
![]()
ПРИКЛАД 2.
Розставити границі інтегрування в тому і в другому порядку в подвійному інтегралі
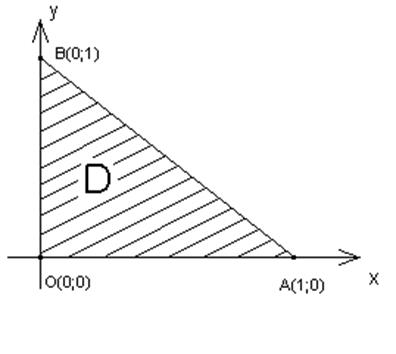
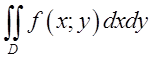 , де
, де ![]() -
трикутник з вершинами
-
трикутник з вершинами ![]() .(рис.1).
.(рис.1).
Розв’язок: побудуємо область. Запишемо рівняння ліній, які обмежують область: ![]() це осі. Рівняння прямої
це осі. Рівняння прямої ![]() будемо
шукати у вигляді:
будемо
шукати у вигляді: 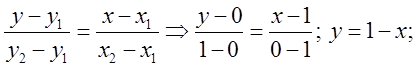
Розпишемо подвійний інтеграл
через повторний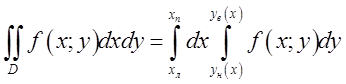 ;де Рис.4.5.
;де Рис.4.5.
![]() ;
;![]() -
(індекси внизу ікса - означають крайня ліва і крайня права координата області
по змінній х) визначити дуже легко;
-
(індекси внизу ікса - означають крайня ліва і крайня права координата області
по змінній х) визначити дуже легко; ![]() - це
значення змінної
- це
значення змінної ![]() , яке приймає поточна (текущая)
точка, знаходячись в крайній лівій частині області
, яке приймає поточна (текущая)
точка, знаходячись в крайній лівій частині області ![]() .
Аналогічно
.
Аналогічно ![]() -
це значення змінної
-
це значення змінної ![]() , яке приймає поточна точка
знаходячись в крайній правій частині області
, яке приймає поточна точка
знаходячись в крайній правій частині області ![]() . В
нашому випадку
. В
нашому випадку ![]() . Значення
. Значення ![]() і
і ![]() - (нижнє
і верхнє) знайти важче, бо вони будуть залежати від тих значень змінної
- (нижнє
і верхнє) знайти важче, бо вони будуть залежати від тих значень змінної ![]() , які вона приймає в межах попереднього
інтегрування. Обчислимо їх декілька, використовуючи рівняння границь області і
застосовуючи рисунок 1. При
, які вона приймає в межах попереднього
інтегрування. Обчислимо їх декілька, використовуючи рівняння границь області і
застосовуючи рисунок 1. При 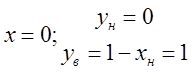 ; при
; при 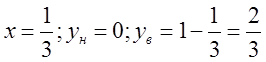 ; при
; при ![]() ;
; ![]() ми
знаходимо, підставляючи
ми
знаходимо, підставляючи ![]() в рівняння, яке обмежує
область
в рівняння, яке обмежує
область ![]() знизу;
знизу; ![]() ми
знаходимо, підставляючи
ми
знаходимо, підставляючи ![]() в рівняння, яке обмежує
область
в рівняння, яке обмежує
область ![]() згори. А тому в загальному випадку в
другому інтегралі границями повинні стояти функції
згори. А тому в загальному випадку в
другому інтегралі границями повинні стояти функції ![]() і
і ![]() ; Відповідь:
; Відповідь: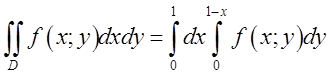 .
.
ПРИКЛАД 3.
Перемінити порядок інтегрування в повторному інтегралі
![]()

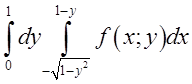
![]()
![]()








![]()
 Розв’язок: випишемо рівняння ліній, які обмежують область інтегрування
Розв’язок: випишемо рівняння ліній, які обмежують область інтегрування ![]() :
: ![]() ,
або
,
або ![]() при
при ![]()
![]() , або
, або ![]() .
Зобразимо область
.
Зобразимо область![]() (рис.4.6). Областю буде криволінійний трикутник
(рис.4.6). Областю буде криволінійний трикутник ![]() . Якщо змінна
. Якщо змінна ![]() буде
змінюватись від
буде
змінюватись від ![]() до
до ![]() то
змінна величина
то
змінна величина ![]() буде змінюватись від
буде змінюватись від ![]() в точці
в точці![]() до
0 в точці
до
0 в точці![]() .
. ![]() , за величиною буде дорівнювати висоті стовпчика
, за величиною буде дорівнювати висоті стовпчика![]() , яка буде залежати від того значення
, яка буде залежати від того значення ![]() в якому знаходиться точка
в якому знаходиться точка![]() .Очевидно, що для інтервалу зміни
.Очевидно, що для інтервалу зміни ![]() від
від ![]() до
до
![]() значення
значення ![]() буде
увесь час
буде
увесь час
Рис 4.6.
дорівнювати![]() . В цей час
. В цей час ![]() буде зростати від
буде зростати від![]() до
до![]() , причому, це зростання
йтиме вздовж дуги кола
, причому, це зростання
йтиме вздовж дуги кола ![]() , або
, або ![]() . Так буде до тих пір доки
точка
. Так буде до тих пір доки
точка ![]() не дійде до
не дійде до![]() . (В цей час точка
. (В цей час точка![]() дійде до точки
дійде до точки ![]() ). В точці
). В точці ![]() порушується умова гладкості
кривої, бо в ній невизначена похідна . В точці
порушується умова гладкості
кривої, бо в ній невизначена похідна . В точці ![]() точка
точка ![]() переходить з
кривої
переходить з
кривої ![]() на лінію
на лінію ![]() . З цієї причини ми вимушені,
користуючись властивістю адитивності подвійного інтеграла , розбити його на два
інтеграли: один по області
. З цієї причини ми вимушені,
користуючись властивістю адитивності подвійного інтеграла , розбити його на два
інтеграли: один по області![]() ,
четвертина кола
,
четвертина кола ![]() ; другий по області
; другий по області
![]() ; частина площини першого
квадрату обмежена трикутником
; частина площини першого
квадрату обмежена трикутником ![]() . В
інтегралі по області
. В
інтегралі по області ![]()
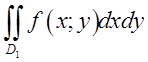
![]() змінюється від
змінюється від![]() до
до ![]() в зовнішньому інтегралі і
в зовнішньому інтегралі і ![]() змінюватиметься від
змінюватиметься від ![]() до
до ![]() у внутрішньому, тобто :
у внутрішньому, тобто :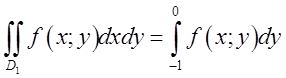 . Для кращого розуміння
розстановки границь можна, як до прикладу технічної реалізації ідеї, звернутись
до роботи телевізора. Якщо горизонтально відхиляюча система електроніки промінь
буде відхиляти від точки
. Для кращого розуміння
розстановки границь можна, як до прикладу технічної реалізації ідеї, звернутись
до роботи телевізора. Якщо горизонтально відхиляюча система електроніки промінь
буде відхиляти від точки ![]() до точки
до точки ![]() , то щоб одержати на екрані
зображення сектора
, то щоб одержати на екрані
зображення сектора ![]() , треба у
вертикальному напрямку промінь ганяти від прямої
, треба у
вертикальному напрямку промінь ганяти від прямої ![]() до кривої
до кривої ![]() . Якщо
протягом одного відхилення по горизонталі буде виконуватись декілька сот
відхилень по вертикалі, то рисочки
. Якщо
протягом одного відхилення по горизонталі буде виконуватись декілька сот
відхилень по вертикалі, то рисочки ![]() зільються і ми одержимо зображення сектора. Аналогічно,
зільються і ми одержимо зображення сектора. Аналогічно, 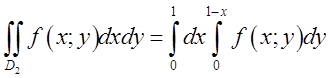 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.