Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 3

3.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 642-670.

3.6. На практичному занятті використовуються формули, таблиці, теореми.

          1). Означення функціонального ряду.                    

О. Функціональним називається ряд

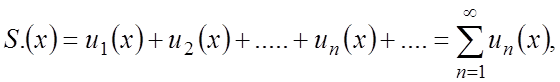
          (1.3)

де всі функції  визначені на певній множині, наприклад X. Як і для числових рядів

О. Функціональний ряд (1.3) називається збіжним при х=х₀, якщо відповідний числовий ряд, утворений з ряду (1) при х=х₀, є збіжним.

          О. Функціональнийряд (1.3) називається збіжним на множині Х, якщо він збіжний

          Т. (Вейерштрасса). Якщо  х всі члени ряду (1.3) задовольняють нерівність  причому ряд  збіжний, то ряд (1.3) рівномірно збіжний на

2). Властивості рівномірнозбіжних рядів.

Т. 1. (неперервність суми). Сума рівномірно збіжного на  ряду, складеного з неперервних на  функцій, є неперервною на  .

Т. 2.(про граничний перехід). Рівномірно збіжний на  ряд допускає на цьому інтервалі граничний перехід для , тобто .

Т. 3.(про диференціювання ряду). Збіжний на  ряд допускає на цьому інтервалі по членне  диференціювання за умови, що одержаний ряд буде рівномірно збіжний на , тобто .

3). Застосування степеневих рядів у точних та наближених обчисленнях. Теорема Абеля.

О. Степеневим рядом називають ряд 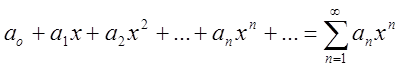    (2.3)

Ряд (2)  називають рядом за степенями х. Тут

О. Степеневим також називають ряд 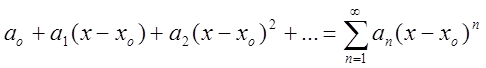   (3.3)

Т.а) Якщо степеневий ряд (2.3) збіжний при  то він абсолютно збіжний і при  таких, що

б) Якщо степенний ряд (2.3) розбіжний при , то він розжбіжний і при  таких, що .

3.7. Вправи на засвоєння матеріалу

1).  Розв’яжемо декілька прикладів:

 ПРИКЛАД 1.

   Знайти область збіжності ряду: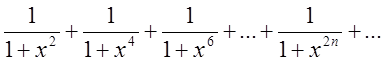

Розв’язання:

треба дослідження ряду на збіжність розкласти на 3 випадки: якщо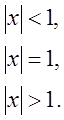  

1) 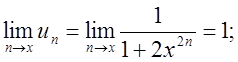  таким чином    ряд розбіжний.

2) 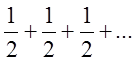 -  ряд розбіжний, бо .

3) 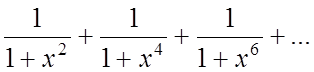члени даного ряду менш, ніж члени нескінченно спадної геометричної прогресії 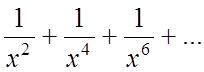, тому ряд збіжний на цьому проміжку.

Відповідь: ряд збіжний, якщо

ПРИКЛАД 2.

Показати, що ряд 

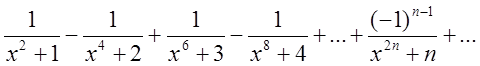
   рівномірно збіжний у випадку 

Розв’язання:

 Даний ряд при всякому значенні x збіжний за ознакою Лейбніца, тому залишок оцінюється за допомогою нерівності таким чином

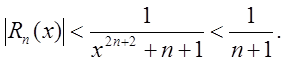
Нерівності 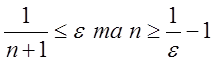  рівносильні,   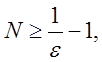прийдемо до нерівності

Відповідь: ряд справді збіжний у даному проміжку.

ПРИКЛАД 3.

Показати, що ряд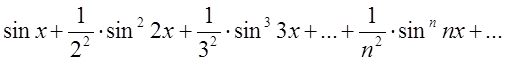 

рівномірно  збіжний у проміжку

Розв’язання:

Скористатися ознакою Вейєрштрасса:

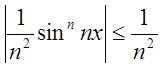 і ряд 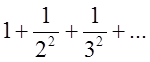збіжний, тому ряд збіжний при всякому значенні x.

Відповідь: ряд збіжний при всякому значенні x.

Розвинути в ряд за степенями x функцію .

Розв’язання:

Спочатку треба знайти значення функції та її похідних при x=0:

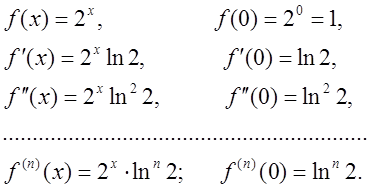
 тому при фіксованому x має місце нерівність для всіх n.

Функція можна представити у формі суми ряду Маклорена:

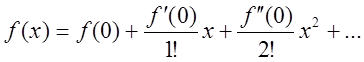 у даному випадку питання про збіжність ряду вирішується ознакою Даламбера.

Відповідь: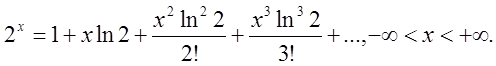

2). Розв’язати самостійно:

1.Знайти інтервал збіжності степеневого ряду і дослідити його збіжність на кінцях інтервалу.

1.1. 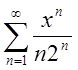; Відп. .1.2. 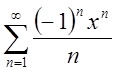;Відп.1.3. 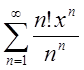; Відп..

2. Розвинути в ряд за  степенями х вказані функції та знайти область їх збіжності.

2.1. 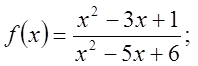 Відп. , .

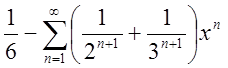2.2. Відп. .

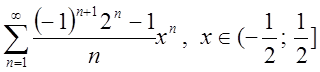3. Обчислити з точністю до 0,001, застосовуючи ряди.

3.1.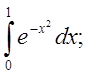Відп. 0,7468.      3.2.  Відп.  2,087. 

Практичне заняття 4.

План:

4.1.Тема. Дослідження рядів Тейлора та Маклорена. Розвинення деяких функцій в степеневі ряди. Застосування степеневих рядів у точних та наближенних обчисленнях.

4.2.Ціль:

1). Засвоїти ряди Тейлора та Маклорена.

2). Засвоїти застосування функцій в степеневі ряди.

3). Засвоїти формулу Єйлера.

4). Засвоїти застосування степеневих рядів у точних та наближених обчисленнях.

4.3. Теоретичний матеріал подано в лекції номер 2.

4.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).