11.6. На практичному занятті використовуються формули, таблиці, теореми.
2). Умови незалежності інтеграла від лінії інтегрування.
Лема. Для того щоб криволінійний інтеграл 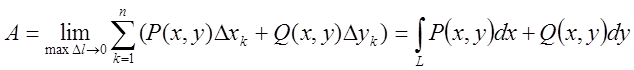
не залежав від лінії інтегрування, необхідно і достатньо, щоб цей інтеграл, узятий по будь-якому замкнутому контурі, дорівнював нулю.
Теорема 1. Якщо
функції ![]() і їхні частинні похідні неперервні в однозв'язній області Q і в усіх її точках виконується рівність
і їхні частинні похідні неперервні в однозв'язній області Q і в усіх її точках виконується рівність 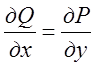 , то
вираз
, то
вираз![]() є повним диференціалом.
є повним диференціалом.
Теореми 2. Нехай
функції ![]() неперервні разом зі своїми частинними
похідними в поверхово однозв'язній області
неперервні разом зі своїми частинними
похідними в поверхово однозв'язній області ![]() . Тоді
рівносильні наступні твердження:
. Тоді
рівносильні наступні твердження:
1. Криволінійний інтеграл 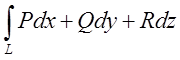 , узятий по будь-якому замкнутому
контуру, що цілком лежить в області
, узятий по будь-якому замкнутому
контуру, що цілком лежить в області ![]() , дорівнює нулю.
, дорівнює нулю.
2. Криволінійний інтеграл 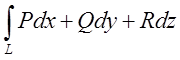 не залежить від лінії інтегрування, що
з'єднує дві дані точки.
не залежить від лінії інтегрування, що
з'єднує дві дані точки.
3. Вираз ![]() є повним диференциалом.
є повним диференциалом.
4. В усіх точках області ![]() має місце рівність
має місце рівність 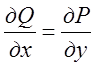 ;
;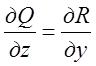 ;
;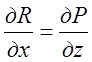 .
.
3). Формула Ньютона – Лейбніца.
Формулу ![]() тобто
тобто 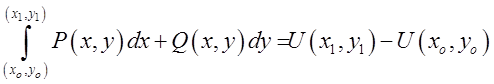
називають формулою Ньютона-Лейбніца для криволінійного інтеграла від повного диференціала.
Формула Ньютона-Лейбніца для криволінійного інтеграла від повного диференціала в трьохвимірному просторі має вид:
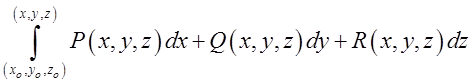 =
=
=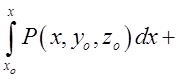
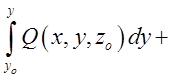
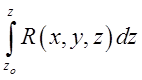 .
.
11.7. Вправи на засвоєння матеріалу.
1). Розв’яжемо декілька прикладів:
2)Розвязати самостійно.
1.Обчислити криволінійні інтеграли від повниз диференціалів:
а) 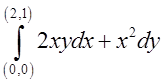 .Відп.
.Відп.![]() б)
б)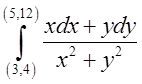 .Відп.
.Відп.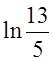 . в)
. в)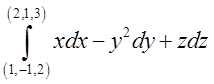 .Відп.
.Відп.![]() .
.
2. Знайти функції за заданими повними диференціалами:
а) 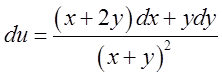 . Відп.
. Відп.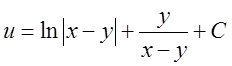 .
.
б) 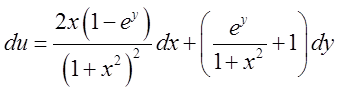 . Відп.
. Відп.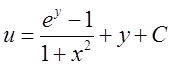 .
.
в) 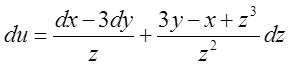 . Відп.
. Відп. 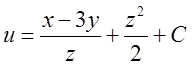 .
.
Практичне заняття 12.
План:
12.1.Тема. Дослідження поверхневих інтегралів за координатами. Їх властивостей. Обчислення поверхневих інтегралів.
12.2.Ціль:
1). Засвоїти інтеграл по поверхні.
2). Засвоїти теорему і формулу Стокса.
3). Засвоїти формулу Остроградського – Гауса.
12.3. Теоретичний матеріал подано в лекції номер 10.
12.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).
12.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 481-490.
12.6. На практичному занятті використовуються формули, таблиці, теореми.
1). Інтеграл по поверхні.
Інтеграл
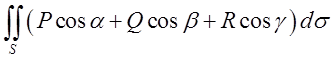
і будемо називати інтегралом по поверхні.
Означення. Інтегралом по поверхні (або поверхневим інтегралом) називається границя інтегральної суми
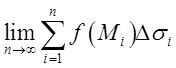 =
=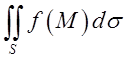 =
=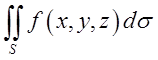
при прямуванні до нуля діаметра кожної площадка розбивки.
При зміні напрямку нормалі на протилежний, ми від поверхневого
інтегралу по одній стороні поверхні переходимо до поверхневого інтегралу по
протилежній стороні, а значить можемо записати для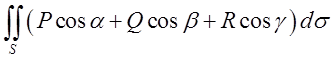
дуже важливу властивість
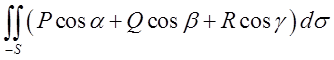 =
=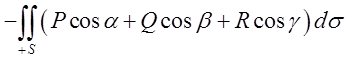
2) Теорема і формула Стокса.
Теорема.
Нехай функції ![]() неперервні разом зі
своїми частинними похідними в деякій тривимірній області. Тоді для будь-якої
гладкої поверхні S, що лежить у цій області, має місце формула
неперервні разом зі
своїми частинними похідними в деякій тривимірній області. Тоді для будь-якої
гладкої поверхні S, що лежить у цій області, має місце формула
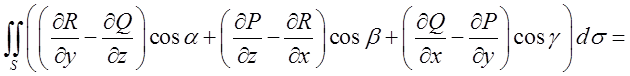
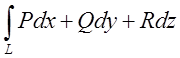
де ![]() напрямні косинуси нормалі до поверхні S, а L-границя поверхні.
напрямні косинуси нормалі до поверхні S, а L-границя поверхні.
Ця формула називається формулою Стокса.
Формула Стокса дозволяє інтеграл по поверхні замінити відповідним криволінійним інтегралом по границі поверхні і, навпаки, криволінійний інтеграл по замкнутій просторовій лінії замінити інтегралом по поверхні натягнутій на контур інтегрування.
3). Формула Остроградського – Гауса.
Теорема.
Нехай функції ![]() неперервні разом зі
своїми частинними похідними в деякій замкнутій області
неперервні разом зі
своїми частинними похідними в деякій замкнутій області ![]() ,
тоді має місце формула
,
тоді має місце формула
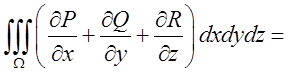
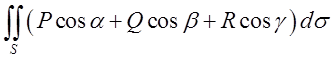
де S-границя області ![]() і інтегрування по S
проводиться по її зовнішній стороні (
і інтегрування по S
проводиться по її зовнішній стороні (![]() -напрямні косинуси
зовнішньої нормалі). Ця формула називається формулою Остроградского-Гауса.
-напрямні косинуси
зовнішньої нормалі). Ця формула називається формулою Остроградского-Гауса.
Формула Остроградского дозволяє замінити потрійний интеграл відповідним інтегралом по поверхні, яка обмежує область інтегрування і, навпаки, інтеграл по замкнутій поверхні замінити потрійним інтегралом по області обмеженою цією поверхнею.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.