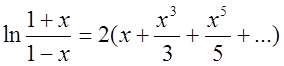Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 5

Одержимо робочу формулу . Обчислимо при якому значенні х вираз під логарифмом дорівнює 3. 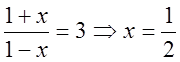. Підставивши це значення в робочу формулу одержимо =

Щоб досягти заданої точності достатньо взяти суму перших чотирьохчленів. Остача ряду буде   

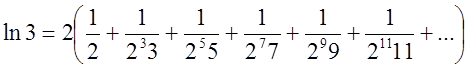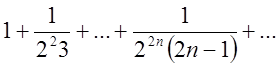
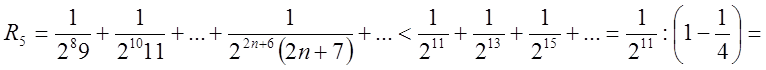
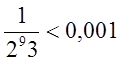=. А тому .

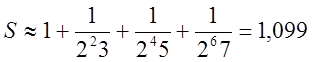Практичне заняття 5.

План:

5.1.Тема.  Дослідження тригонометричної системи функцій. Тригонометричні ряди Фур’є для періодичних функцій з періодом , збіжність. Тригонометричні ряди Фур’є для періодичних функцій з довільним періодом, для парних і непарних функцій.

5.2.Ціль:

1). Засвоїти тригонометричні ряди Фур’є. Теорема Діріхлє.

2). Теорема Діріхлє.

3). Засвоїти розвинення в ряд по несиметричному прорміжку.

4). Засвоїти розвинення в ряд по довільному симетричному проміжку .

5). Засвоїти комплексну форму запису ряду Фур’є.

5.3. Теоретичний матеріал подано в лекції номер 3.

5.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).

5.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 691-704.

5.6. На практичному занятті використовуються формули, таблиці, теореми.

          1). Тригономерричні ряди Фур’є. Теорема Діріхлє.

О. Система функцій  називається ортогональною в інтервалі , якщо інтеграл від добутку двох різних функцій системи дорівнює нулю: .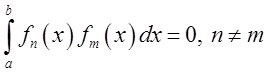

Квадрат довжини функції  (  називають нормою) визначають так: 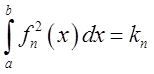. Якщо тепер кожну із системи ортогональних функцій розділимо на її норму, то одержимо ортонормовану (функції попарно взаємно перпендикулярні і кожна з них має одиничну довжину) систему функцій 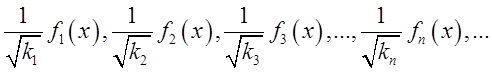 бо кожні дві з них залишилися перпендикулярними і тепер уже 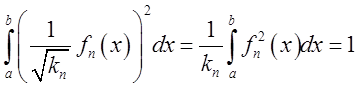. Безпосередньою перевіркою можна переконатися, що система функцій 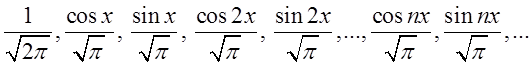є ортонормованою на проміжку , а значить , задану на цьому проміжку, можна розкласти за цією системою: 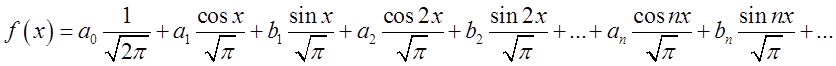.Щоб знайти коефіцієнти  досить домножити обидві частини вищенаписаної рівності на 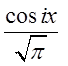або  на  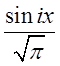 і проінтегрувати. Так наприклад щоб знайти  домножимо обидві частини  рівності на 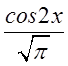 і проінтегруємо. 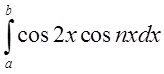Так як система функцій ортогональна, то при  всі інтеграли  і 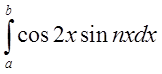  дорівнюють нулеві і залишиться тільки 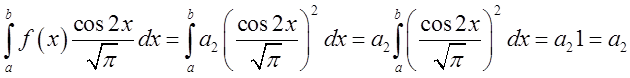. Аналогічно ми можнмо знайти який-завгодно коефіцієнт. А тому сформулюємо наступне твердження.

Нехай функцію  задано на проміжку , тоді цю функцію можна розвинути в тригонометричний ряд, який має назву ряд Фур’є і має такий вид: 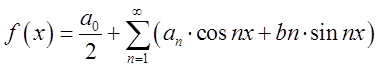   ;      (5.1)

де коефіцієнти  обчислюють за формулами:

;   ;

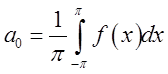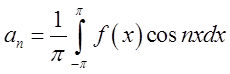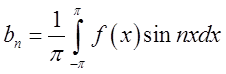 ; при чому                                           (5.2)

         2). Теорема Діріхлє про розвинення  функції в ряд Фур’є

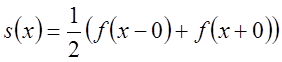Якщо функція на інтервалі ; є         1)кусочномонотонна; 2) кусочнонеперервна; 3) обмежена, то її  тригонометричний ряд Фур’є збігається в усіх точках сегмента . Якщо  – сума тригонометричного ряду Фур’є функції  , то в усіх точках неперервності цієї функції , а в усіх точках розриву . Крім того  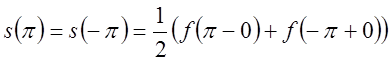                                                      (5.3)

          3). Розвинення в ряд по несиметричному проміжку.

Через те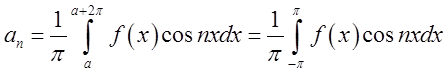  

     Спочатку пригадаємо той факт, що якщо функція  має період то:

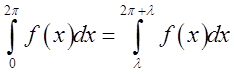. Через те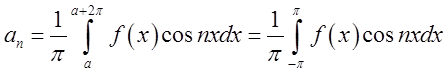  

     (при  )               

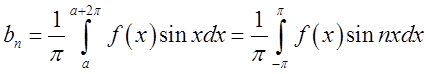
          4). Розвинення в ряв по довільному симетричному проміжку     

Якщо задана функція  де то для неї ряд Фур’є має вид:

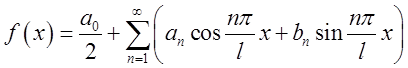                                                    (3.5)

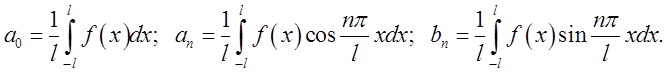               (3.6)  

5). Комплексна форма запису ряду Фур’є.

Формули Эйлера дозволяють виражати тригонометричні функції через показникові функції з комплексним показником. Отже, у такій комплексній формі можуть бути представлені тригонометричні ряди і, зокрема, ряди Фур'є тих чи інших функцій.

 Нехай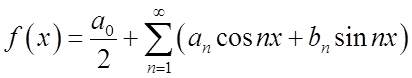                                        (3.7)

– деякий тригонометричний ряд. Ми маємо формули Эйлера

      .

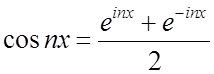
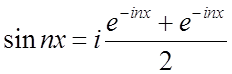 Тоді 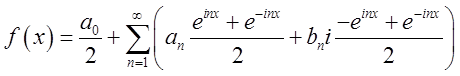  , або поєднуючи степені з однаковими показниками, 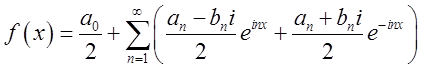 .                                              (5.10)