2.3.1. Построение моделей очистки масел на отечественном сорбенте
Сначала необходимо сформировать модель описываемого процесса [34]. В целом изучалась зависимость вида:
СВ = f (d, N), (2.1)
где СВ – остаточное содержание восков в масле после очистки;
d – средний размер кристаллов ВС в масле, мкм;
N – штучная концентрация кристаллов в пробе масла.
Следует отметить вновь, что параметры d и N здесь служат исходными данными для расчета эффективности фильтрации растительных масел, поэтому при проведении расчетов их можно считать независимыми (п. 1.4).
В случае же введения в систему каолина, как показали предварительные исследования, точки, отвечающие экспериментальным данным, лежат в одной плоскости. Это означает, что построение модели предусматривает использование линейного уравнения регрессии для двух переменных:
![]() ,
(2.2)
,
(2.2)
где Y – значение (отклик) уравнения регрессии;
X1, Х2 – факторы уравнения регрессии, а именно средний размер кристаллов ВС (d) и их штучная концентрация (N) соответственно;
а1, a2, a3– коэффициенты уравнения регрессии.
Решение поставленной задачи сводится к определению неизвестных коэффициентов уравнения регрессии (2.2).
Расчеты проводили в табличном процессоре MSExcel с использованием средств VBA (Visual Basic for Application). Суть сводилась к составлению и решению системы уравнений, куда в качестве неизвестных входили коэффициенты из уравнения (2.2):
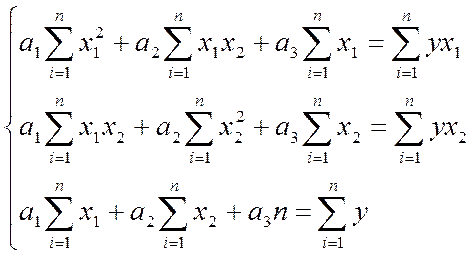 ,
(2.3)
,
(2.3)
где n – количество опытов, учитываемых при обработке.
Систему (2.3) решали методом Гаусса с выбором главного элемента. Пример расчетного листа документа MSExсel для определения параметров уравнения регрессии приведен на рис. 2.3. Исходные данные представлены во втором-четвертом вектор-столбцах, где значение функции Y отвечает остаточному содержанию ВС в испытуемом масле, а размер кристаллов и их штучная концентрация соответствуют Х1 и Х2. В левый столбец входят номера опытов.
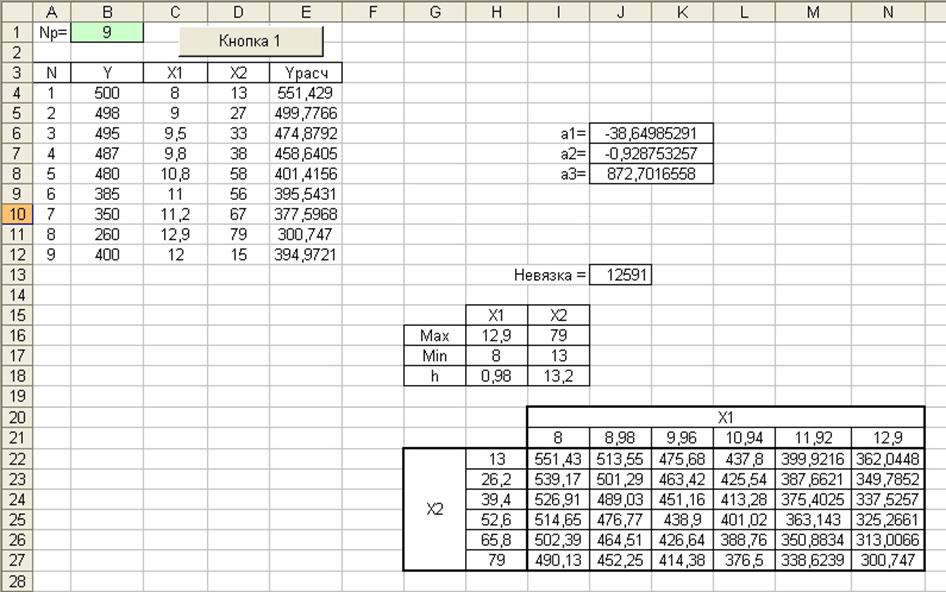
Рис. 2.3. Пример расчетного листа MSExсel для определения
параметров уравнения регрессии (на примере льняного масла)
После внесения опытных данных в указанные столбцы нажимают кнопку 1, и автоматически производятся необходимые действия, включая графическую интерпретацию результатов, помещаемых в правую часть расчетного листа (см. рис. 2.3). Считывание данных, их обработку и вывод итогов на лист производят в программном модуле, представленном в Приложении. Программный модуль – по сути дела, макрос (код, интегрированный в книгу MSЕxcel), совмещающий процедуры ввода-вывода параметров и реализации вышеуказанного алгоритма.
Таким образом, была получена модель влияния параметров ненаправленной кристаллизации на очистку масел от восков. Эта модель представляет собой удобный инструментарий для дальнейшего исследования и оптимизации процесса очистки.
2.3.2. Математическая модель выделения восков на природном каолине
Опыты проводили на образцах соевого, льняного и оливкового масел. В качестве сорбента использовали природную каолиновую глину. Ее фракционный состав представлен на рис. 2.4.
Полученные экспериментальные данные по очистке различных видов масел сведены в табл. 2.8.
Найдем коэффициенты уравнения регрессии, решив систему (2.3) (табл. 2.9). Анализ приведенных в табл. 2.9 данных показывает, что таковые воспроизводимы на различных образцах, поскольку порядок приведенных коэффициентов близок друг другу.
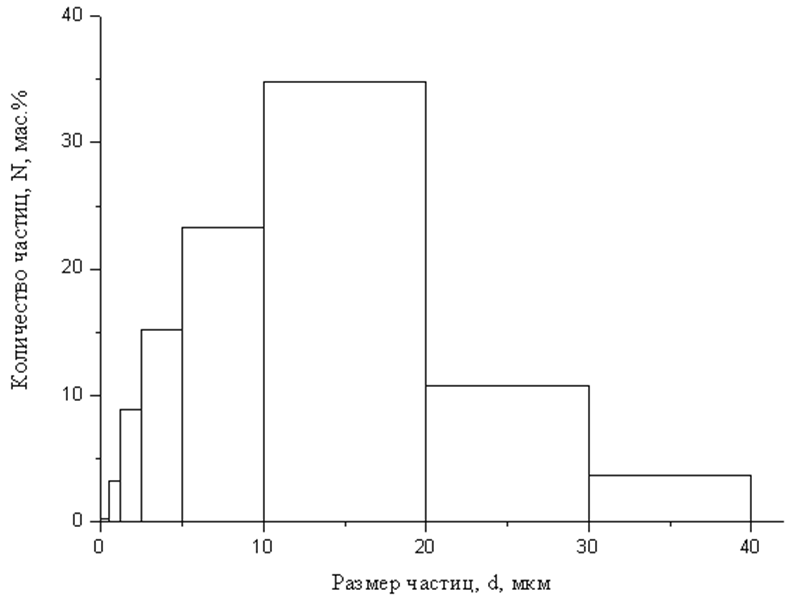
Рис. 2.4. Фракционный состав белой (каолиновой) глины (Самарская область)
Таблица 2.8
Результаты эксперимента по изучению очистки масел от восков
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.