Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 9

Верхня половина діаграми на рис. 2.5,б відображає нумерацію клітинок на діаграмі функції трьох змінних, а один верхній рядок – на діаграмі функції двох змінних аналогічно як і на діаграмах Венна (див. рис. 2.4,ж,б).

Діаграми функцій п’ятьох і більше змінних можна побудувати аналогічно, подвоєнням попередніх діаграм (рис. 2.6,а,б,в). Так, для п'ятьох змінних координаті х5=0 відповідає ліва відносно жирної осі півдіаграма (див. рис. 2.6,а), що повторює діаграму функції чотирьох змінних, а права пів-  діаграма (при х5=1) нумерується дзеркально відносно осі (початок нумерацій виділено). Аналогічно за допомогою координати х6 ( рис. 2.6,в) утворюється діаграма функції шістьох змінних.

Діаграму, як і таблицю відповідності, можна побудувати  й  за  будь-яким іншим способом задання функції, наприклад, за формулою ДДНФ або ДКНФ, бо кожній одиниці або нулю діаграми однозначно відповідає свій терм. Так, одиниці в лівому верхньому кутку діаграми на рис. 2.6,б відповідає мінтерм 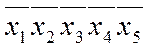, а нулю в правому верхньому кутку діаграми на рис. 2.5,г – макстерм  згідно з правилами входження змінних до термів ДДНФ та ДКНФ.

2. Правила мінімізації.ДДНФ функції m змінних зображається як логічна сума всіх мінтермів рангу m, тобто добутків усіх m змінних або їх інверсій. Методи мінімізації ґрунтуються на наслідку склеювання (10а в табл. 2.2), який можна узагальнити таким чином:

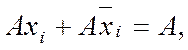                                                                                                             (2.13)

де А – будь-який вираз, зокрема, добуток змінних. Отже, склеюватися можуть мінтерми, які відрізняються лише значенням однієї змінної: в одному з них хi=0, а в іншому хi=1. Саме так розташовано терми в діаграмах: сусідні клітинки (які знаходяться поруч по горизонталі й вертикалі або по краях діаграми) відрізняються лише однією змінною, тому дві одиниці в сусідніх клітинках склеюються графічно, утворюючи сполуку, що відповідає мінтермові нижчого рангу.

Графічна мінімізація за допомогою діаграм термів полягає в об’єднанні клітинок за правилами: 1) об’єднувати можна сусідні одиничні клітинки, утворюючи сполуки по 2k=2, 4, 8,... одиниць, причому одна й та сама одиниця може входити до кількох сполук, а якщо якась одиниця не має сусідніх, вона утворює сполуку з однієї клітинки; 2) усі одиниці мають бути охоплені (покриті) сполуками таким чином, щоб, по-перше, кожна з них об’єднувала найбільшу кількість одиниць та, по-друге, діаграма містила найменшу кількість сполук; 3) будь-якій одиничній клітинці відповідає первісний мінтерм рангу m, а    кожній сполуці з 2k клітинок відповідає вкорочений мінтерм рангу m-k, що є добуток тільки тих змінних, які мають стале значення для всієї сполуки, причому змінна  входить до мінтерма без інверсії, якщо її значення є одиниця (є риска проти всієї сполуки на діаграмі), та з інверсією – якщо нуль (риска відсутня); 4) отже, мінімізована функція є логічна сума всіх утворених мінтермів – сполук одиниць.

Здебільшого існує багато варіантів утворення сполук. Оптимізувати процедуру мінімізації доцільно таким чином. 1) Якщо є одиничні клітинки, які можна приєднати до інших лише одним способом, найкраще розпочати      об'єднувати саме з таких клітинок. У прикладі на рис. 2.5,в більш, ніж одну сусідню мають усі одиничні клітинки (показано пунктиром), крім десятої (нумерацію клітинок подано на рис. 2.5,б). Тому утворюємо сполуку (1) приєднанням цієї клітинки до восьмої. 2) Після цього розглядаємо можливість утворити об’єднання з найбільшої кількості одиниць по 2k. Так, на нашій діаграмі  сполуку з 8 елементів утворити не можна, тому 4 одиниці об’єднуємо до квадрата (2). 3) Відтак із ще не охоплених одиниць утворюємо інші сполуки або приєднуємо вільні одиниці до вже утворених сполук так, щоб мінімальною кількістю сполук охопити (покрити) усі  одиниці. У прикладі сполука (3) охоплює решту одиниць. Якщо варіантів рівноцінних сполучень кілька, занотовуємо їх для можливого використання на останньому етапі проектування. 4) І, нарешті, зчитуємо мінтерми з утворених сполук. Так, сполука (1), складена з двох первісних мінтермів четвертого рангу, утворює мінтерм третього рангу , до якого змінні x₁, x₃входять з інверсією тому, що проти всієї сполуки (1) немає їх рисок, та змінна x₄ входить без інверсії тому, що проти всієї сполуки розташована її риска, а змінна x₂ до мінтерма не входить через те, що її значення не є сталим протягом сполуки (проти клітинки 10 є риска, а проти клітинки 8 риска відсутня). Чотири одиниці сполуки (2) відповідають мінтермові другого рангу x₁x₃, до якого входять змінні x₁ і x₃ без інверсії, бо проти всієї сполуки є риски цих змінних, а змінні x₂, x₄ до сполуки не входять, бо їх значення змінюються протягом сполуки. Аналогічно зчитуємо мінтерм зі сполуки (3): . Підсумовуванням мінтермів дістаємо шукану МДНФ  у вигляді