Вирази у0, у1 подано в нестандартній, мішаній формі, бо в стандартній формі вираз має містити лише елементи булевого базису у вигляді або суми добутків (диз’юнкції кон’юнкцій), або добутку сум (кон’юнкції диз’юнкцій). Саме такою є функція у2, зображена в диз'юнктивній формі (ДФ), тому що вона є диз’юнкцією над елементами виразу (термами), кожний з яких містить тільки операції кон’юнкції та інверсії. На відміну від неї, функція у3 подана в диз'юнктивній нормальній формі (ДНФ), бо її терми містять операції інверсії над окремими змінними, але не над виразами. І, нарешті, зображена
Згідно з дуальністю алгебри логіки аналогічно можна зобразити функцію в кон’юнктивній (КФ), кон’юнктивній нормальній (КНФ) та досконалій кон’юнктивній нормальній формі (ДКНФ). ДКНФ функції являє собою кон’юнкцію термів, кожний з яких є диз’юнкція над усіма літералами, наприклад, як у виразі у5.
З огляду на те, що одна й та сама змінна не може бути поданою в жодному термі двічі (згідно з аксіомами це не має сенсу), логічна функція в ДДНФ або ДКНФ має тільки єдине зображення, тому вона є зручною стандартною моделлю репрезентування функції у формалізованих методах перетворень.

2. Мінтерми й макстерми. Розглянемо для прикладу функцію, задану таблицею відповідності
(табл. 2.3). Зобразімо її спочатку за допомогою добутків усіх літералів.
Виходимо з того, що на будь-якому вхідному кортежі функція як добуток літералів
набуває значення у=1 лише одним способом: до добутку входять змінні без
інверсії, якщо в цьому кортежі вони мають значення 1, і з інверсією, якщо їх
значення дорівнює 0. Такі добутки називають мінтермами (конституентами
одиниці); у прикладі їх два: М1=![]() , M2=
, M2=![]() . Отже, мінтерми
утворюються за одиничними значеннями функції як добутки літералів
. Отже, мінтерми
утворюються за одиничними значеннями функції як добутки літералів
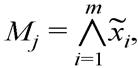
де ![]() – літерал, m
– кількість змінних. ерез те, що кожний мінтерм перетворює функцію на одиницю
тільки на своєму кортежі, а на всіх інших кортежах він дорівнює нулю, усю
функцію можна зобразити як логічне додавання мінтермів
– літерал, m
– кількість змінних. ерез те, що кожний мінтерм перетворює функцію на одиницю
тільки на своєму кортежі, а на всіх інших кортежах він дорівнює нулю, усю
функцію можна зобразити як логічне додавання мінтермів
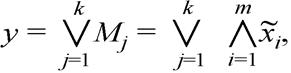
де k – кількість мінтермів, тобто одиниць у колонці функції її таблиці відповідності. У прикладі маємо відомий вираз для функції виключне АБО
![]() (2.2)
(2.2)
зображеної в ДДНФ.
Розмірковуючи аналогічно, з таблиці легко знайти також вираз для інверсної функції в ДДНФ за нулевими її значеннями (тобто одиницями в колонці y):
![]() (2.3)
(2.3)
Так само можна зобразити
функцію в ДКНФ, якщо виходити з добутку сум літералів. Диз’юнкція літералів, де
функція перетворюється на нуль, назиається макстермом (конституентою
нуля), тому до макстерма змінна входить без інверсії, якщо її значення в
кортежі дорівнює нулю, інакше – з інверсією. У прикладі є два макстерми: М0' =x1+ x2 , М3' =![]() . Або взагалі
. Або взагалі
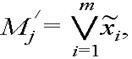
а вся функція зображається в ДКНФ через кон’юнкцію макстермів
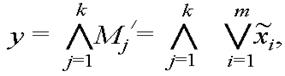
де k – кількість макстермів, тобто нулів у колонці функції її таблиці відповідності. Отже, у прикладі маємо ДКНФ
![]() (2.4)
(2.4)
Аналогічно можна знайти вираз для інверсної функції в ДКНФ за одиничними значеннями (тобто нулями в її колонці):
![]() (2.3)
(2.3)
Таким чином, будь-яка логічна функція зображається в ДДНФ або ДКНФ єдиним способом, тому ці форми є вихідними для подальшого аналізу й синтезу. Інші стандартні форми ДНФ і КНФ можуть бути простішими, ніж відповідні досконалі форми, проте в них функції зображаються багатьма способами, що утруднює алгоритмізацію їх перетворень. Принципово обидві досконалі форми рівноцінні, але ДДНФ є зручніша для побудови пристроїв у базисі І-НЕ, а ДКНФ – у базисі АБО-НЕ. Через більшу поширеність елементів І-НЕ у складі сучасних мікросхем, а також більш звичні співвідношення алгебри логіки (формули з літерою а в табл. 2.2), частіше вживається ДДНФ зображення функцій.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.