Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 14

Аби полегшити подібні перетворення, далі розглядаються окремі прийоми схемної мінімізації, тобто способи зменшення складності логічної схеми. Як показник її складності за звичай використовується потрібна кількість корпусів q_к однотипних ІС. На стадії логічного проектування відносно простих схем користуються показником складності структурної функції у вигляді суми  q=q_е+q_в потрібної кількості логічних елементів q_е та загальної кількості їх входів q_в (іноді складність зручніше оцінювати  потрібною загальною кількістю зовнішніх виводів інтегрованих мікросхем q_з.в). Проте наочним для порівняння схем і зручним під час їх технічної реалізації на логічних елементах (на вентильному рівні) є показник у вигляді зазначення через риску кількості елементів на загальну кількість їх входів q=q_е /q_в, яким і користуватимемося далі.

Складність легко оцінити безпосередньо з виразу підрахуванням кількості логічних операцій та змінних (літер), що входять до кожної з них. Так, у виразі (2.2) маємо два елементи І та один АБО по два входи кожний, а також два інвертори по одному входу, тобто разом q=5/8 (див. рис. 2.9,а). У виразах, перетворених до базисів І-НЕ та АБО-НЕ, досить підрахувати кількість знаків інверсії (елементи) та змінних під кожним з них (входи).

2. Редукція в диз'юнктивній формі. Якщо об'єднанню до сполук з більшої кількості одиниць на діаграмі термів заважають окремі нулі, функцію можна спростити, розглядаючи спочатку ці нулі як одиниці, а відтак скоригувати її вилученням з множини одиниць зайві нульові клітинки. Систематизовану процедуру такого спрощення називають редукцією. У загальному вигляді під час мінімізації в ДНФ редукцію можна виконати доповненням заданої функції у неперетинною з нею допоміжною функцією у₁ таким чином, аби об'єднання D цих функцій та сама допоміжна функція у₁були якомога простішими. Тоді, на підставі (2.9) шукану функцію дістаємо з виразу

                                                                                       (2.19)

Так, мінімізацією звичайним чином функції, заданої діаграмою 1 на            рис. 2.13,а

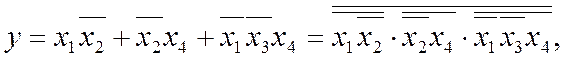
маємо реалізацію її в базисі І-НЕ складністю q=7/13. Редукцію виконуємо в такий спосіб. Введенням допоміжної функції y₁=x₁x₂(зазначена зірочками) мімімізуємо утворене об'єднання (на діаграмі обведено)

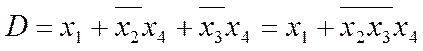
і за (2.19) у підсумку отримуємо структурну функцію

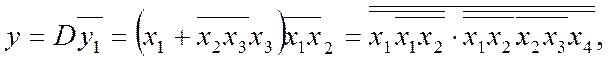
яка реалізується мінімальною схемою в базисі І-НЕ складністю q=5/11             (рис. 2.13,б).

З метою спрощення допоміжної функції до неї можна долучити інші ну-льові клітинки (якщо вони є), які не входять до об'єднання. При цьому корекція за виразом (2.19) не змінює функцію, бо згідно з операцією заборони 0\1=0.

Якщо в нашому прикладі утворити об'єднання, обведене на діаграмі (2) D=x1+x4, то для вилучення зайвих клітинок, позначених зірочками, до допоміжної функції (пунктир) додаємо ще шосту клітинку:  y1=x1x2+x2x3. У підсумку маємо шукану функцію

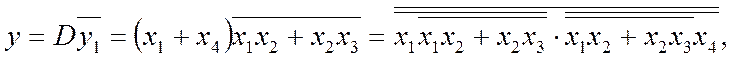
яка реалізується мінімальною схемою з використанням елемента І-АБО-НЕ складністю q=4/10 (рис. 2.13, в).

Цілком зрозуміло, що редукцію можна застосувати і не до функції в цілому, а лише до її фрагменту, якщо така процедура приводить до мінімальнішої форми. Тоді, під час коригування фрагменту за (2.19) до допоміжної функції з метою її спрощення можна долучити одиничні клітинки, що перетинаються з рештою функції. Це означає, що мінтерм, охоплений однією сполукою одиниць, не обов'язково повторювати в інших сполуках.

У прикладі на діаграмі (3) частину функції x4 (верхня половина діаграми) не має потреби коригувати, а з решти одиниць та нульової клітинки, поміченої зірочкою, утворюємо об'єднання D=x1+x3 (обведено суцільною лінією). Для вилучення нульової клітинки до допоміжної функції y1=x1x2x3 додаємо ще   сьому клітинку, бо вона вже репрезентована у функції частиною . Отже, маємо структурну функцію

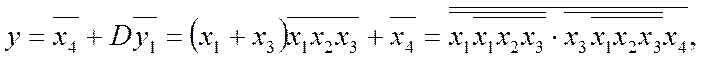                                                                                                            (2.20)

для реалізації в базисі І-НЕ за мінімальною схемою (рис. 2.13,г) складністю q=4/10 (проти 7/13 або 6/12 у варіантах без редукції).