Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 23

Заваду можна зменшити до припустимого рівня також за допомогою згладжувального фільтра типу інтегрувального кола (пунктир на рис. 2.18,а). Проте через погіршення швидкодії такого заходу вживають рідко, в основному, для виявлення місця виникнення завади: якщо з приєднанням до виходу у невеликої ємності викид зменшується (пунктир на рис. 2.18,г), слід усунути змагання сигналів на входах елемента.

Запитання та вправи

2.1. Які системи логічних функцій є функціонально повні? Які з них є мінімально повні? Доведіть, що мінімально повну систему утворюють: 1) операція заборони і константа одиниці, 2) операція імплікації і константа нуля.

2.2. Які є відмінні риси зображення логічних функцій, притаманні таким формам: мішаній, ДФ, ДНФ, ДДНФ, МДНФ, КФ, КНФ, ДКНФ, МКНФ?

2.3. Який  логічний елемент B утворюється  послідовним з'єднанням (умовно позначимо його знаком +) елементів НЕ на кожному з двох входів елемента A або (та) на його виході таким чином: а) A+НЕ=B, б) НЕ+A=B, в) НЕ+A+НЕ=B, якщо A є елемент: 1) АБО, 2) І, 3) виняткове АБО, 4) НІ, 5) АБО-НЕ, 6) І-НЕ, 7) виняткове АБО-НЕ, 8) імплікатор? Зобразіть 24 такі схеми.

2.4. Шляхом тотожних перетворень доведіть еквівалентність схем, поданих на рисунках: 2.9,а,б; 2.10,ж; 2.11,ж; 2.12,б; 2.13,д,е та за допомогою аналогічних перетворень наведіть паралельні схеми для елемента виняткове АБО-НЕ.

2.5. Доведіть співвідношення: 1) 8...12 з табл. 2.2; 2) ; 3);  4); 5); 6); 7); 8); 9) y1\(y1\y2)=y2\(y2\y1);

10) y2\(y1y2)=(y1+y2)\y1; 11) y1+(y2\y1)=y1+y2; 12) y1y2+(y2\y1)=(y1+y2)\(y1\y2);

13) y1y2Ìy1+y2; 14) y1 Ì y2, якщо y1y2=y1 або y1+y2=y2 або y1 =0; 15) y3 Ì y1 та

 y3 Ì y2, якщо y1y2=y3; 16) y1=, якщо y1+y2=1 та y1y2=0; 17) , якщо y1+y2=1 та y1y2 ¹0; 18) , якщо y1y2=0; 19) y1\y2=y1 та  y2\y1=y2, якщо y1y2=0; 20) , якщо y2 Ì  y1. Співвідношення 7...20 проілюструйте графічно діаграмами Венна.

2.6. Спростіть вирази: 1) ; 2) ; 3) ; 4) ; 5); 6) ; 7); 8) . Вказівка. За необхідністю, скористайтеся діаграмами термів.

2.7. Мінімізуйте логічну функцію за методом Квайна - Мак-Класкі, яка набуває значення лог. 1 на кортежах i: 1) 3, 4, 5, 7, 9, 11, 12, 13; 2) 1, 3, 5, 7, 9, 11, 15; 3) 0, 2, 3, 5, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, а на всіх інших кортежах – лог. 0; 4) якщо на кортежах, зазначених у п.3 цієї вправи, функція набуває значення лог. 0, а на всіх інших – лог. 1.

2.8. Для функції, заданої таким чином: 1) словесно: y=1, якщо , тобто якщо код, утворюваний двома старшими бітами вхідного кортежу, більший або дорівнює кодові з його двох молодших бітів; 2) множиною мінтермів ={M₁, M₄, M₅, M₇}, а M₀, M₂, M₃, M₆Ï; 3) діаграмою термів D₃₅ на рис. 2.14,б; 4) схемою по виходу y₆ на рис.2.14,в; 5) функцією довільної форми: y=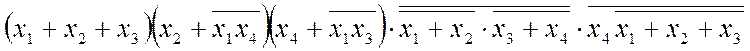; 6) нулями на діаграмі термів у клітинках i=0, 1, 4, 10, 11, 14, 16, 17, 20, 26, 27, 30 та всіма іншими одиницями; 7) одиницями в зазначених у п.6 цієї вправи клітинках i діаграми та нулями в усіх інших; 8) y=1 на кортежах i=1, 2, 5, 6, 8, 11, y=0 при i=0, 7, 9, 10, 13 та невизначену на інших кортежах, наведіть мінімальні форми для побудови схеми в базисах: а) булевому в послідовності НЕ, І, АБО; б) булевому в послідовності НЕ, АБО, І; в) І-НЕ; г) АБО-НЕ; д) І-АБО-НЕ; е) у мішаній формі, за змогою з використанням елементів виключне АБО(-НЕ). Визначте складність та швидкодію схем.

2.9. Мінімізуйте схему в елементному базисі І-НЕ чи АБО-НЕ, який забезпечує меншу складність (на чотирьох логічних елементах за однофазного надходження змінних), для заданої логічної функції: 1) ;

2) ; 3) ; 4); 5) ; 6); 7) ; 8); 9) ; 10) .

2.10. Виконайте спільну мінімізацію чотирьох вихідних функцій, що здійснюють перетворення ДДК 8421 згідно з табл. 1.6, 1.7 у такі коди: а) 2421, б) 7421, в) 8421+3 (з надлишком три), г) код Ґрея (перші десять цифр X₁₀=0...9 чотирирозрядного коду). Вказівки. На заборонених кортежах X₁₀>9 вважати функції невизначеними. Схему мінімальної складності реалізуйте на довільних логічних елементах.