Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 7

1. Графічна ілюстрація операцій над логічними функціями. Розглядатимемо логічну функцію як множину y={M_i}, елементами якої є мінтерми M_i, що відповідають значенню y=1 на певних вхідних кортежах i. Усі 2^m можливих

Якщо якась функція є константою нуля yº0, що відповідає порожній множині y=Æ, то всю діаграму займає ділянка 0, а якщо вона є константою одиниці yº1, то вся діаграма збігається з ділянкою 1. Отже, співвідношення між частинами діаграми для довільної функції зображається як =1\y чи y=1\y, бо область визначення U=y+º1.

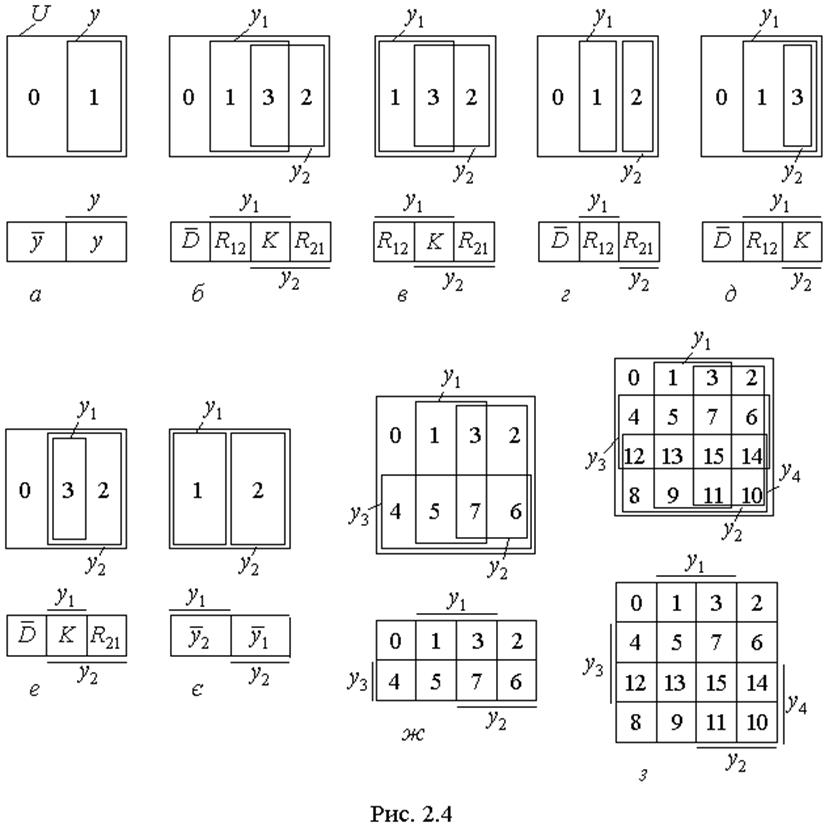
На діаграмі рис. 2.4,б зображено дві функції y₁ і y₂, подані прямокутниками, а на спрощеній нижній діаграмі обидві функції подано рисками. Нумерація ділянок діаграми відповідає десятковим кодам, складеним з цих функцій, наприклад, ділянка, де перетинаються обидві функції, має код і=у₂у₁=11₂=3₁₀, а ділянка, де у₂=1, у₁=0 – номер і=у₂=10₂=2₁₀.

На цій діаграмі ділянки відповідають таким логічним операціям над функ-ціями: 1, 3, 2 – диз'юнкція чи об'єднання (АБО) D=y₁+y₂; 0 – інверсія або доповнення об'єднання (АБО-НЕ) ; 3 – кон'юнкція або перетин (І) K=y₁y₂; 0, 1, 2 – доповнення перетину (І-НЕ) ; 1 – різниця (заборона) R₁₂=y₁\y₂, яка утворюється вилученням з прямокутника y1 тих одиниць, що збігаються з функцією y₂; 2 – аналогічна різниця R₂₁=y₂\y₁; 0, 2, 3 – імплікація y₁®y₂=R₁₂; 0, 1, 3 – аналогічна імплікація y₂®y₁=; 1, 2 – сума за модулем два (виключне АБО) M=y₁Åy₂; 0, 3 – виключне АБО-НЕ .

Як видно з діаграми, підмножина мінтермів, яка утворює перетин функцій (ділянка 3), входить до складу підмножини об'єднання (ділянки 1, 3, 2), що позначається символом включення KÌ D. Отже, завжди KD=K. Виражаючи подібним чином операції одна через одну, дістанемо співвідношення:

   

(2.6)

2. Зв'язок між функціями і їх складниками. Якщо одну з двох функцій, наприклад, y₁ вважати відомою, то за допомогою операцій (2.6) можна виразити шукану функцію y₂ через відому або її окремі складники, що є, по суті, розв'язанням логічного рівняння відносно невідомої змінної. Безпосередньо з діаграми Венна (див. рис. 2.4,б) видно, що пряма функція y₂  утворюється логічним підсумовуванням ділянок 2, 3, а інверсна – ділянок 0, 1. Отже, потрібно виразити ці ділянки через величини, які вважатимемо відомими, бо їх можна визначити з таблиці відповідності. Залежно від співвідношення між функціями розглянемо такі випадки.

а) У загальному випадку (див. рис. 2.4,б) з урахуванням (2.6) матимемо

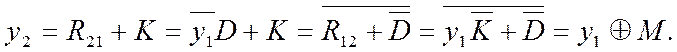                                                                                                            (2.7)

Ці вирази мають універсальний характер, бо яку з порівнюваних функцій вважати відомою y1, а яку – шуканою y2, не має значення, аби-но їх назви в (2.6) і (2.7) були однаковими. Вирази (2.7) в окремих випадках співвідношення між функціями можна спростити.

б)  У   разі   суцільногопокриттяобласті   визначення   обома   функціями

(рис. 2.4,в), тобто якщо D = 1, K ¹ 0, дістанемо

                                                                                           (2.8)

в) Ознакою неперетинних функцій (рис. 2.4,г) є K=0, а також R12=y1, R21=y2, тому

                                                                                                                                     (2.9)

Зауважимо, що при цьому співвідношення y1\y2=y1, y2\y1=y2 можуть виявитися корисними для спрощення логічних виразів.

г) У випадку включення шуканої функції до складу відомої y2Ìy1 (рис. 2.4,д), коли D=y1, K=y2, R21=0, маємо

                                                    (2.10)

д) Навпаки, за включення відомої функції до складу шуканої y1Ì y2      (рис. 2.4,е), коли D=y2, K=y1, R12=0, маємо

y2=y1+R21.                                                               (2.11)

е) І, нарешті, ознакою взаємоінверсних функцій (рис. 2.4,є) є D=1, K=0, отже,

y2=D\ y1=.                                                                (2.12)