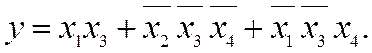Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 10

                                                                       (2.14)

Цю ж саму діаграму термів можна використати й для здобуття інверсної функції КНФ, якщо сполуки зчитувати як такі, до яких змінні входять із протилежним значенням (риска відповідає нульовому значенню аргумента, а її відсутність – одиничному). Так, безпосередньо з діаграми на рис. 2.5,в зчитуємо МКНФ інверсної функції

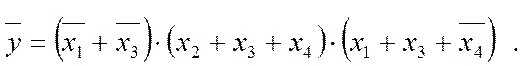
Очевидно, цей вираз можна дістати згідно з (2.1) і безпосередньо з формули МДНФ (2.14), якщо вона є.

Методика мінімізації в КНФ за допомогою діаграм термів не відрізняється від розглянутої з урахуванням лише особливостей (див. рис. 2.5,г): об’єднують до сполук клітинки  з нулями та до складу макстермів змінну зчитують з інверсією, якщо проти сполуки є її риска і, навпаки, без інверсії, якщо риска відсутня. Тому МКНФ функції має вигляд:

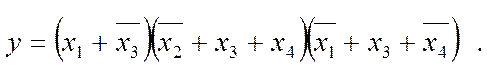                                                       (2.15)

Інверсну функцію МДНФ також можна отримати з цієї самої діаграми, зчитуючи сполуки нулів так само, як сполуки одиниць:

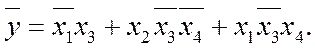
або, якщо є, безпосередньо з МКНФ згідно з (2.1).

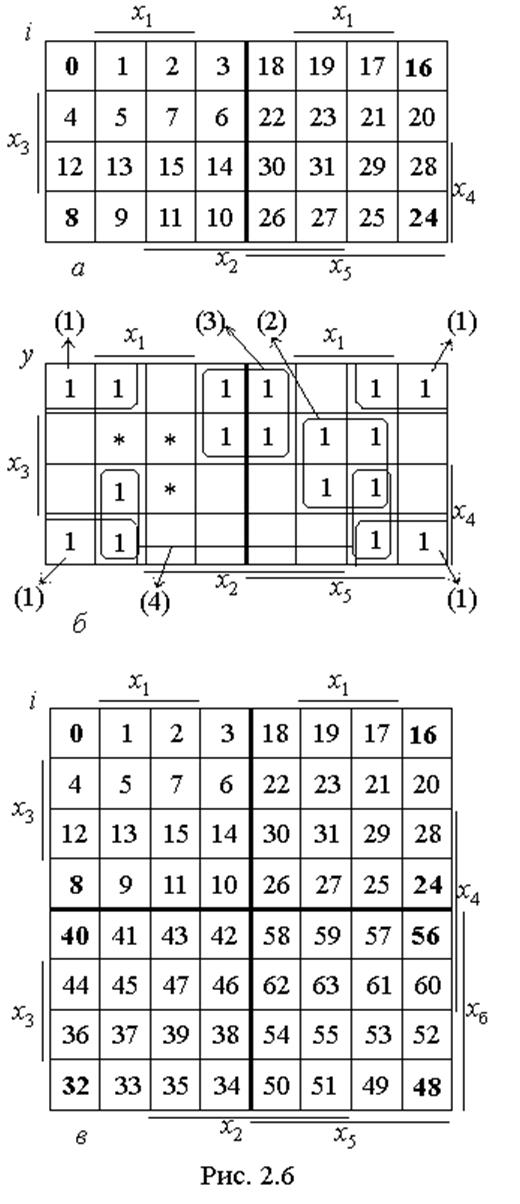
3. Особливостімінімізаціїзізбільшеннямкількостізмінних. На будь-якій діаграмі кожна клітинка має m сусідніх (m – кількість змінних), розташованих, наприклад, для функції чотирьох  змінних ліворуч, праворуч, вгорі та знизу, включаючи крайні. Для функції п’ятьох змінних (див. рис. 2.6,а) крім чотирьох на своїй півдіаграмі додається ще п’ята сусідня клітинка на другій півдіаграмі, розташована симетрично відносно осі симетрії (жирна лінія), з кодом i+16, тобто сусідньою відносно, наприклад, п’ятої буде ще двадцять перша клітинка, а для функції шістьох змінних (рис. 2.6,в) сусідньою з п'ятою є ще тридцять сьома клітинка. Взагалі, зі збільшенням кількості змінних на одиницю крім попередніх додається ще одна симетрична клітинка з кодом i+2m-1 на сусідній півдіаграмі. Саме це ускладює процедуру мінімізації функцій зі збільшенням кількості змінних.

Полегшити мінімізацію можна, впорядкувавши цей процес. Розглянемо його на прикладі діаграми п’ятьох змінних (рис. 2.6,б).

1) Утворюємо спочатку сполуки клітинок на одній півдіаграмі, наприклад, правій, де одиниць більше. У прикладі здобуваємо сполуки 1,2 з чотирьох елементів кожна (та ще беремо під увагу не помічену другу від правого краю колонку), а також сполуку 3 із двох одиниць.

2) Уявно перегинаючи діаграму по осі симетрії, перевіряємо, чи не накладаються утворені сполуки на такі самі групи клітинок лівої півдіаграми. Так, сполука 1 віддзеркалена на лівій півдіаграмі чотирма симетричними клітинками, які й приєднуємо до цієї сполуки тепер вже з 8 одиниць; квадрат 2 пов-ністю не відображається на лівій півдіаграмі (показано зірочками) та колонка одиниць на ній розірвана, тому на правій півдіаграмі залишаємо сполуку 2 з чотирьох елементів, яка охоплює більше вільних одиниць, ніж колонка. Дві клітинки правої півдіаграми об’єднуються із симетричними на лівій, утворюючи сполуку 3 з чотирьох одиниць.

3) Переходимо до лівої півдіаграми й утворюємо так само сполуки з вільних одиниць, приєднуючи їх за змогою до інших сполук спочатку своєї, а відтак симетричної правої півдіаграми. У прикладі є одна вільна одиниця в клітинці i=13, яка приєднується до іншої (i=9) зі сполуки 1, утворюючи сполуку 4 з двох одиниць. Перевірка на симетрію з одиницями правої півдіаграми (обведено) збільшує сполуку 4 до чотирьох одиниць на двох півдіаграмах.

4) Зчитуючи сполуки по черзі, записуємо вираз для МДНФ функції:

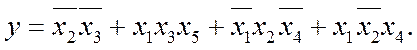
Принагідно зауважимо тут, що діаграму можна заповнити за процедурою, зворотною зчитуванню термів під час мінімізації. Якщо функція задана в мішаній формі, спочатку перетворюємо її до нормальної форми (ДНФ або КНФ). Відтак визначаємо групи клітинок, що відповідають кожному термові і вносимо їх до діаграми. Наприклад, перший терм ДНФ (2.14) визначає квадрат одиниць (2) на діаграмі (див. рис. 2.5, в), проти якого є риски змінних x₁, x₃; другому термові відповідає сполука (3), проти якої відсутні риски змінних x₂, x₃, x₄  і т. ін. Так само від КНФ (2.15) легко перейти до діаграми (див. рис. 2.5, г) з урахуванням входження змінних до термів.