Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 15

3. Редукція в кон'юнктивній формі.Враховуючи дуальність алгебри логіки щодо логічних функцій І та АБО, аналогічну редукцію можна виконати і під час мінімізації в КНФ. Але тепер до нульових клітинок функції у з метою спрощення їх сполук на діаграмі долучаємо ще деякі одиничні клітинки, утворюючи допоміжну функцію у1, якщо доповнення об'єднання  цих функцій (тобто сполучення нульових і ще приєднаних одиничних клітинок) і нова функція у1 виявляються простими. Для здобуття шуканої функції необхідно в утвореному об'єднанні відновити одиничні клітинки, тобто виконати операцію імплікації

                                                                                           (2.21)

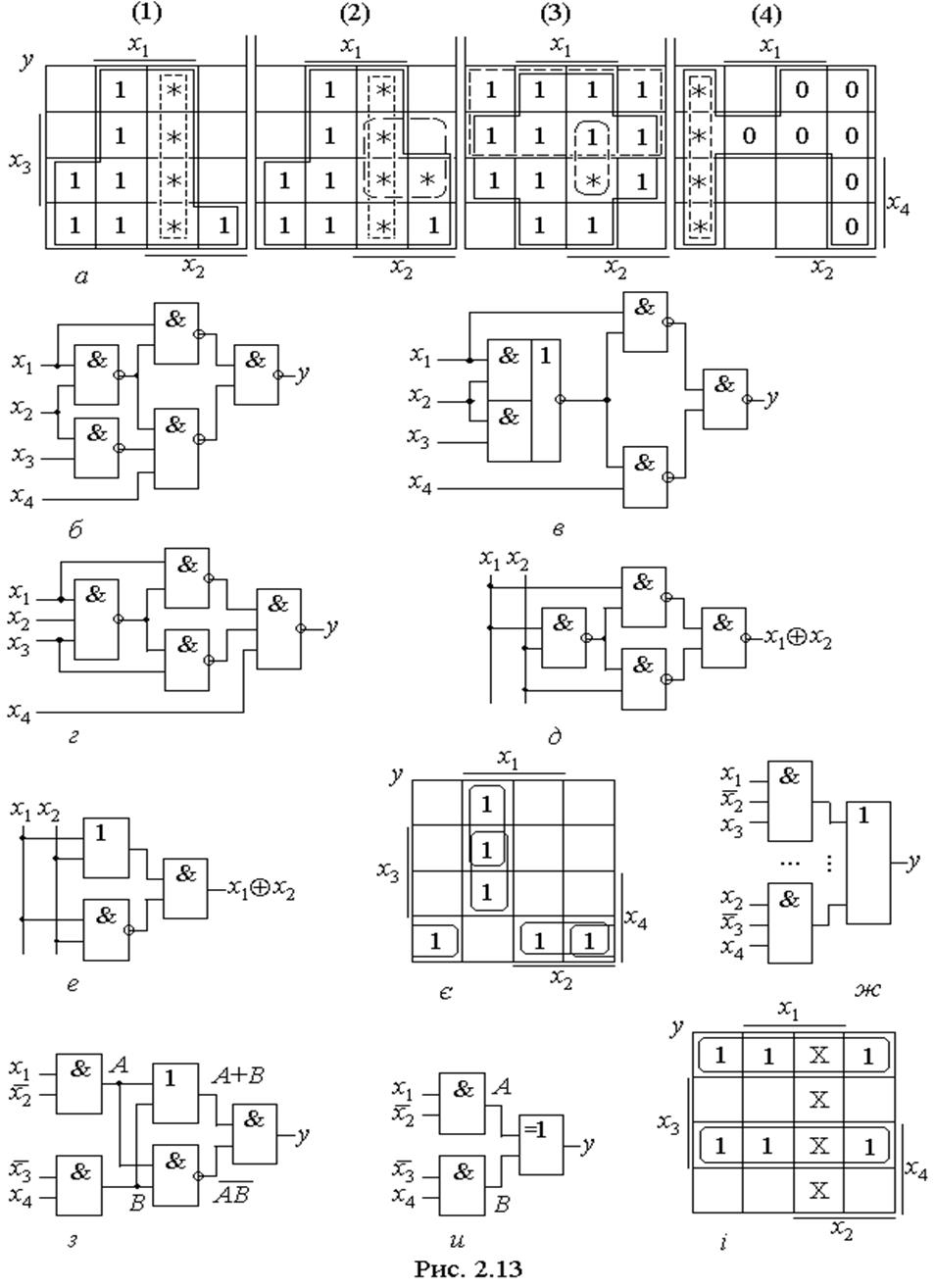
Так, МКНФ функції, що задана діаграмою (4) на рис. 2.13,а, перетворена до базису АБО-НЕ, відповідає складності q=7/13:

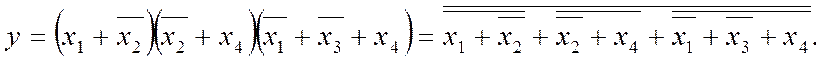
Для редукції спочатку з одиничних клітинок (помічені зірочками) утворюємо допоміжну функцію, яку (вважаючи ці клітинки нульовими) зображаємо в МКНФ: у1=х1+х2. Відтак долученням цих клітинок до нульових утворюємо доповнення об'єднання (обведено суцільною лінією) і також мінімізуємо його в МКНФ:

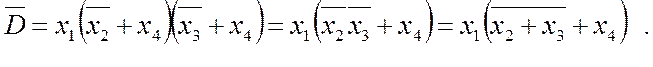
Нарешті, за (2.21) дістаємо спрощений вираз шуканої функції

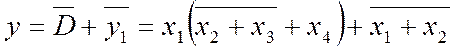
та користуючись розподільчим законом ab+c=(a+c)(b+c) переходимо до базису АБО-НЕ

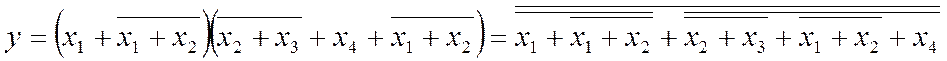
зі складністю q=5/11 (відповідає схемі на рис. 2.13, б, якщо елементи І-НЕ замінити на АБО-НЕ).

4. Алгебричне виконання редукції.Наведена в п. 2, 3 графічна процедура редукції за допомогою діаграм термів є наочною і практично не потребує тотожних перетворень. Природно, у простих випадках редукція виконується і алгебрично. Інколи перетворення спрощуються шляхом мінімізації в МКНФ функції для реалізації в базисі І-НЕ та в МДНФ – для реалізації в базисі АБО-НЕ. Наприклад, об'єднанням нулів на діаграмі 3  рис. 2.13, а,  одержуємо  МКНФ і за розподільчим законом (8б у табл. 2.2) зводимо до виразу

від якого легко перейти до (2.20).

Алгебрично редукцію виконувати доцільно у випадку різного входження однакових змінних (без інверсії та з інверсією) до кількох термів безпосередньо за формулами в диз'юнктивній та кон'юнктивній формах відповідно:

                                                                 (2.22)

                                     (2.23)

астосовуючи двічи перетворення за цими формулами, наприклад, до (2.2), (2.5)

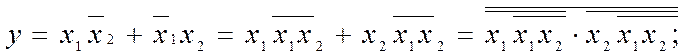               (2.24)

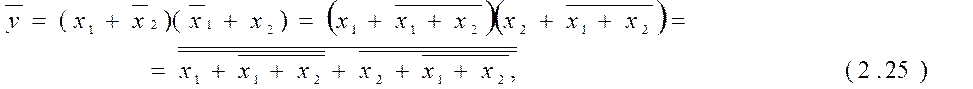дістанемо мінімальні схеми реалізації функцій виняткове АБО та виняткове АБО-НЕ відповідно в базисах І-НЕ та АБО-НЕ складністю 4/8. На рис. 2.13 д наведено одну з двох цих дуальних схем.

Узагальнюючи, можна дійти висновку, що процедура редукції відображається на схемі додатковим рівнем сполучення логічних елементів. З утворених спрощених сполук діаграми зайві клітинки (разом з приєднаними, за змогою, сусідніми) вилучаються за допомогою тих логічних елементів вхідного рівня, виходи яких є спільними для входів кількох елементів наступного схемного рівня. Це добре видно з наведених прикладів на рис. 2.13,б,в,г,д.

5. Реалізація в мішаній формі.З огляду на те, що сучасні серії інтегрованих мікросхем містять велику номенклатуру типономіналів, для спрощення схем широко використовують різні логічні елементи, тобто практично структурну функцію часто реалізують у мішаній формі.

Передусім, спрощення виконують зменшенням кількості інверсій, зокрема, без переходу до іншого базису. Так, формули (2.3), (2.4) перетворюють у вигляді

 

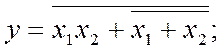
і реалізують без додаткових інверторів як для прикладу на рис. 2.13,е подано схему для другої з цих мінімальних форм.

У мішаній формі з використанням складніших елементів, що виконують різноманітні логічні функції, можна значно спростити схему. Прикладами є вже розглянута реалізація (2.3) в базисі І-АБО-НЕ (див. рис. 2.12,б), а також  відокремлення елемента виняткове АБО наведене в п. 6.

6. Каскадна реалізація термів. Сутність такого спрощення полягає в тому, що в первісному по мінімізації виразі відокремлюють спільні для кількох термів частини винесенням їх за дужки, позначають якимось символом і використовують кілька разів для реалізації функції, внаслідок чого схема в цілому вкорочується.