Для цього складаємо спочатку таблицю (рис. 2.7,д) відповідностей кортежів зі складниками ДНФ – множинами i3, i2: якимось знаком, наприклад, плюс позначаємо, які з кортежів складають кожну з множин. Зокрема, до множини i3=(0,1) як елементи входять набори i=0 та i=1, тому на їх перетині ставимо знак плюс.
 Далі виходимо з того, що всі кортежі i
мають бути репрезентовані в ДНФ таким чином, аби кількість її складників –
множин – була мінімальною. Передусім, природно, залишаємо мінтерми найнижчого
рангу (екстремалі) М2, тобто множини i2 (на рис. 2.7,д обведено), бо вони вбирають
найбільшу кількість мінтермів М4 – кортежів i. Відтак відокремлюємо в таблиці
ще не охоплені (не покриті) кортежі i та множини, до складу яких вони
входять, перебираємо можливі сполучення множин i3, що
охоплюють усі кортежі, та залишаємо тільки мінімальні з цих сполучень. Так,
сполучення по два (0,1) і (0,8), (0,1) і (1,5) не забезпечують покриття, а
(0,1) і (8,10) покривають усі кортежі (у таблиці обведено). Якщо немає таких
сполучень по два, переходимо до сполучень по три, а якщо рівноцінних сполучень
кілька, занотовуємо їх також як варіанти розв’язку задачі.
Далі виходимо з того, що всі кортежі i
мають бути репрезентовані в ДНФ таким чином, аби кількість її складників –
множин – була мінімальною. Передусім, природно, залишаємо мінтерми найнижчого
рангу (екстремалі) М2, тобто множини i2 (на рис. 2.7,д обведено), бо вони вбирають
найбільшу кількість мінтермів М4 – кортежів i. Відтак відокремлюємо в таблиці
ще не охоплені (не покриті) кортежі i та множини, до складу яких вони
входять, перебираємо можливі сполучення множин i3, що
охоплюють усі кортежі, та залишаємо тільки мінімальні з цих сполучень. Так,
сполучення по два (0,1) і (0,8), (0,1) і (1,5) не забезпечують покриття, а
(0,1) і (8,10) покривають усі кортежі (у таблиці обведено). Якщо немає таких
сполучень по два, переходимо до сполучень по три, а якщо рівноцінних сполучень
кілька, занотовуємо їх також як варіанти розв’язку задачі.
5) І, нарешті, як підсумок, записуємо логічний вираз (або вирази, якщо є рівноцінні варіанти) МДНФ з дібраних множин, розшифровуючи їх за кодами з відповідних таблиць М2 та М3:
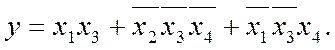
Природно, ця формула збігається з (2.14) і є значно простіша за вихідну ДДНФ.
2. Алгоритм Квайна – Мак-Класкі.За своєю сутністю розглянутий метод не відрізняється від ана літично-табличного методу – алгоритму Квайна – Мак-Класкі. Процедура синтезу за цим методом ще більш формалізована шляхом заміни мінтермів М4, М3, М2 їх цифровими кодами (рис. 2.8,а,б,в): у виразах змінні хi, хi замінено відповідно одиницею або нулем. Якщо під час склеювання утворюється мінтерм нижчого рангу, відсутню змінну (прогалина на рис. 2.7,б,в) замінюємо позначкою Х. Це спрощує запис і уможливлює перетворення на ЕОМ, бо зі збільшенням кількості змінних різко зростає кількість мінтермів, що підлягають перевірці на склеювання. Останній етап мінімізації здійснюється за таблицею, поданою на рис. 2.7,д.
Таким чином, різновиди аналітичних методів мінімізації логічної функції, зокрема, за алгоритмом Квайна – Мак-Класкі полягають у перевірці мінтермів на склеювання та доборі найменшої кількості здобутих скорочених мінтермів (імплікант), які покривають усі первісні мінтерми. Цим здійснюється перетворення від ДДНФ до МДНФ. Метод застосовується, головним чином, для мінімізації функцій з багатьма (не менш, ніж п’ятьма-шістьма) аргументами, особливо на ЕОМ.
§2.3. ОСНОВИ СХЕМНОЇ РЕАЛІЗАЦІЇ ЛОГІЧНИХ ФУНКЦІЙ
2.3.1. Реалізація в поширених базисах
 1. Булів базис.Якщо функція зображена в ДНФ або в
КНФ, то вона містить три елементарні логічні операції над змінними (не над
виразами), що складають булів базис. Схемно такі функції реалізуються
сполученням входів і виходів логічних елементів у послідовності: НЕ, І, АБО
відповідно до формул у ДНФ або в послідовності: НЕ, АБО, І за формулами в КНФ.
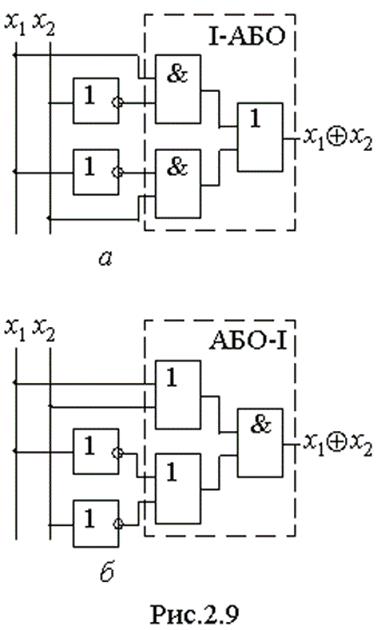
Так, згідно з виразами ДДНФ (2.2) та ДКНФ (2.4) можна побудувати в булевому
базисі елемент виняткове АБО (рис. 2.9,а,б).
1. Булів базис.Якщо функція зображена в ДНФ або в
КНФ, то вона містить три елементарні логічні операції над змінними (не над
виразами), що складають булів базис. Схемно такі функції реалізуються
сполученням входів і виходів логічних елементів у послідовності: НЕ, І, АБО
відповідно до формул у ДНФ або в послідовності: НЕ, АБО, І за формулами в КНФ.
Так, згідно з виразами ДДНФ (2.2) та ДКНФ (2.4) можна побудувати в булевому
базисі елемент виняткове АБО (рис. 2.9,а,б).
Проте зображення схем у булевому базисі, здебільшого, має розглядатися лише як основа для їх порівняння і подальшого перет-ворення до структурної логічної функції. З метою вкорочення схем, використання вільних логічних елементів усередині корпусів частково задіяних мікросхем, зменшення кількості їх типономіналів, зокрема, у потоковому виробництві, а також використання основних і, часто, кращих за параметрами логічних елементів певної серії доводиться перетворювати схеми або їх фрагменти від одного базису до іншого. Для цього розглянемо принципи побудови схем у більш поширених базисах.
2. Базис І-НЕ.Реалізація елементів НЕ, І, АБО, АБО-НЕ (рис. 2.10,а,б,в,г) у базисі І-НЕ випливає безпосередньо зі співвідношень алгебри логіки. Наприклад, за законом двоїстості дістаємо в цьому базисі функцію АБО (див. рис. 2.10,в):
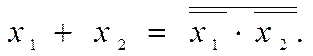
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.