Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 16

Розглянемо такий прийом на прикладі функції, заданої таблицею термів на рис. 2.13,є. За сполуками одиниць дістаємо МДНФ

що реалізується схемою, фрагмент якої наведено на рис. 2.13,ж, складністю q=9/20 з урахуванням вхідних інверторів, які тут і далі не показані. Спрощення виконуємо таким чином. Позначаємо спільні частини , , виносимо їх за дужки та перетворюємо МДНФ з урахуванням (2.22)

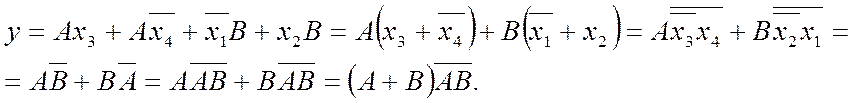
Отже, складність схеми зменшується до q=7/12 (рис. 2.13,з). Якщо доповнити сполуки одиниць долученням дев'ятої клітинки, цього ж висліду можна дійти коротше, процедурою редукції.

Ще більше спрощується схема відокремленням елемента виняткове АБО

складність її становить q=5/8 (рис. 2.13,и).

7. Частково визначені функції.Якщо деякі вхідні кортежі за умов роботи пристрою не виникають, то функція є частково визначеною. Наприклад, у двійково-десяткових кодах (див. табл. 1.6, 1.8) набори змінних при Х₁₀>9 є заборонені, тобто функція на цих наборах лишається невизначеною, що можна тлумачити як байдужі (факультативні) її значення X=0 або 1, бо вони не зустрічаються під час правильної роботи пристрою.

Хай функція чотирьох змінних набуває одиничного значення на кортежах: i=0, 1, 2, 12, 13, 14, крім того, забороненими є кортежі i=3, 7, 11, 15 та нульовими всі інші. На діаграмі термів (рис. 2.13,і) факультативні значення функції помічено позначкою Х. З метою спрощення під час мінімізації функції невизначені умови довизначають таким чином, аби утворювались найбільші сполуки з одиниць, а далі мінімізують як звичайно. У прикладі в двох клітинках, які доцільно приєднати до одиниць, вважаємо X=1, а в двох інших – X=0. Зчитування по утворенні сполук дає спрощену МДНФ

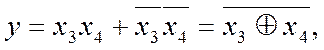
що є функцією виняткове АБО-НЕ. Не важко переконатись, що той самий результат отримаємо об’єднанням на діаграмі нулів і аналогічним довизначенням клітинок X.

Отже, чим більше існує заборонених кортежів, на яких функція є невизначеною, тим більше є можливості для її спрощення.

Таким чином, після мінімізації логічну функцію доцільно додатково спростити для реалізації її з урахуванням потрібного елементного базису. Для цього застосовують перетворення по зменшенню кількості інверсій в термах, переходу до структурної функції в мішаній формі, відокремленню спільних фрагментів у кількох термах з метою їх каскадної реалізації, використанню більш складних елементів, зокрема, типових пристроїв більшого ступеня інтеграції.

2.3.3. Спрощення логічних схем з багатьма виходами

Окрема реалізація функцій для кожного з виходів схем з багатьма виходами, здебільшого, спричиняє нераціональні витрати елементів. З метою оптимальної побудови схеми в цілому вдаються до спільної реалізації сукупності функцій. Для цього логічні функції перетворюють таким чином, аби вони містили спільні частини, тобто виконують каскадну реалізацію шляхом порівняння можливих варіантів і вибору з-поміж них оптимального або, принаймні, прийнятнішого. Такі перетворення виконують аналогічно, як і при каскадній реалізації термів (п.2.3.2), з тією тільки різницею, що спільні частини відокремлюють у кількох функцій. Але шлях подібних перетворень із перебором варіантів може виявитися неозорим для більш-менш складних схем.

Полегшити розв'язання задачі спільної мінімізації можна застосуванням формалізованих способів, два з яких наводяться нижче.

1. Теоретико-множинний спосіб.Спільні частини функцій можна виокремити шляхом використання співвідношень, виходячи з теоретико-множинних уявлень (п.2.1.5). Продемонструємо спосіб на  прикладі спільної мінімізації сукупності функцій з різними типами зв'язку між ними (таблиця відповідності на рис. 2.14,а без колонки j). На рис. 2.14,б компактно зображено 12 діаграм термів: 7 для заданих функцій y₁...y₇ та 5 для співвідношень між цими функціями та їх частинами.

а) Неперетинні функії. Мінімізуємо функції y1, y2, які є неперетинні, бо, як добре видно з їх діаграм, K₁₂=y₁y₂=0 (далі операції між функціями позначатимемо подвійним індексом відповідно до їх нумерації). У цьому випадку згідно з (2.9) для композиції є всього 3 складники: 2 функції, які є невідомі, та диз'юнкція, отже, потрібно мінімізувати два складники і через них виразити третій. Мінімізуємо першу функцію як найпростішу