Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 11

Таким чином, для мінімізації логічних функцій методом діаграм термів (Вайча-Карно) будуємо діаграму з 2m клітинок, позначаємо її координати (нумерацію клітинок) таким чином, аби сусідні геометрично клітинки відповідали сусіднім кодовим наборам змінних та вносимо до діаграми за координатами одиниці (нулі) з таблиці відповідності. Відтак, об’єднуючи одиничні (нульові) сусідні клітинки за певними правилами, утворюємо сполуки, що відповідають мінтермам (макстермам) нижчого рангу та, зчитуючи сполуки, записуємо МДНФ (МКНФ) шуканої функції. Перевага методу полягає в його наочності під час ручного проектування, недолік – в ускладненні процедури мінімізації функцій зі збільшенням кількості змінних.

 2.2.2. Аналітичні методи

1. Формалізований алгебричний метод. Здобуття найкращого або прийнятного варіанту логічної функції алгебрично, шляхом тотожних перетворень займає багато часу й не сповнює впевненістю щодо оптимальності остаточного виразу. Аби уникнути цих недоліків, надамо перетворенням чітко формалізованої послідовності дій і розглянемо їх для наочності на прикладі логічної функції у, що подана таблицею відповідності  (див. рис. 2.5,а).

1) Зобразімо ДДНФ функції у вигляді таблиці мінтермів М₄ (у прикладі – четвертого рангу) з кодами наборів змінних i, що відповідають одиничним значенням функції (рис. 2.7,а). Сума цих мінтермів і становить ДДНФ функції. Згідно з (2.13) склеюватись можуть мінтерми, які відрізняються лише значенням однієї змінної, тому розташуємо їх у таблиці групами за кількістю інверсій змінних або, що те ж саме, нулів у їх кортежах і відокремимо групи рисками: у першій  – чотири інверсії змінних, у другій – три тощо.

2) Внаслідок того, що склеюватись можуть лише мінтерми сусідніх груп, значно зменшується кількість потрібних перевірок на склеювання, які виконуємо послідовно для мінтермів з нумерами  0  і  1,  0  і  8, відтак 1 і 5, 1 і 10 тощо. Якщо результат перевірки позитивний – утворюється мінтерм третього рангу,  вносимо  його до нової таблиці (рис. 2.7,б) мінтермів нижчого рангу М₃ з кодами i3, складеними з кодів склеєних мінтермів вищого рангу М₄. Наприклад, перевірка на склеювання мінтермів з кодами i=0 та 1:  дає мінтерм третього рангу з кодом i₃=(0,1). Коди i можна вважати множинами, що вказують, з яких мінтермів М₄ складаються мінтерми М3. Такий алгоритм передбачає перевірку на склеювання між усіма можливими сполученнями мінтермів, що еквівалентно додаванню одного й того самого мінтерма М4 кілька разів, проте на підставі аксіоми х+х=х функція від цього не змінюється.

3) Далі перевіряємо на склеювання мінтерми М₃, для чого поділяємо їх на групи з однаковими літералами (на рис. 2.7,в відокремлені рисками), бо склеюватись  згідно з (2.13) можуть тільки мінтерми, складені з однакових змінних, одна з яких відрізняється входженням (без інверсії та з інверсією). Перевіряючи на склеювання всі можливі сполучення між мінтермами всередині кожної групи, одержуємо дві такі пари (відмічено квадратними дужками), які утворюють мінтерми меншого, тепер другого рангу М₂, і вносимо їх до таблиці (рис. 2.7,г). У прикладі вони однакові (бо множини i₂ складені з однакових елементів), тому, усуваючи дублікацію, об’єднуємо їх в один мінтерм х₃х₁ (показано дужкою).

Після другого склеювання функція у дорівнює сумі мінтермів М₂ (у нашому випадку він один) і М3, що не увійшли до складу М₂, а  також, якщо є, М₄, що  не  склеїлись  (у  прикладі  таких немає, бо всі коди i є елементами множин i3). Далі

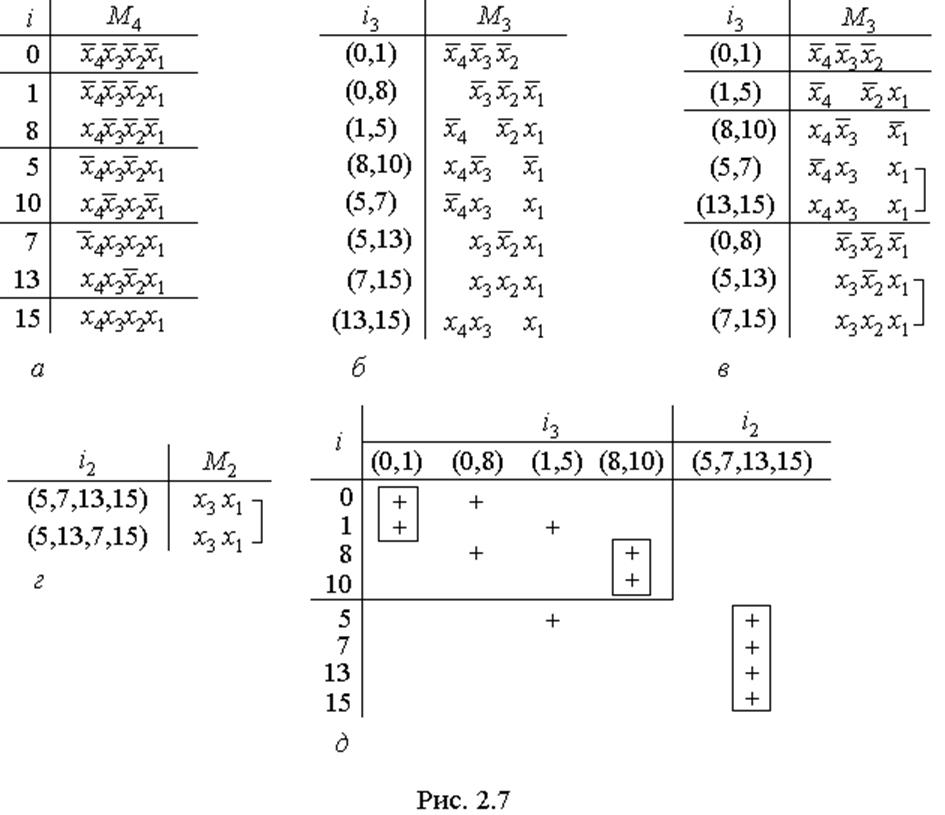
аналогічно продовжуємо склеювання мінтермів меншого рангу доти, поки вони вже не склеюються або залишиться один. У прикладі функція у складається з одного мінтерма М₂ та чотирьох М₃, що не увійшли до М₂.

4) Утворена ДНФ функції є правильною лише тоді, коли на всіх вхідних кортежах i, що відповідають первісним мінтермам ДДНФ М₄, вона обертається на одиницю, а на всіх інших кортежах – на нуль. Проте, якщо вилучення з ДНФ якогось із компонентів, наприклад, одного з мінтермів М₃, не змінює функцію на його кортежі, то він є зайвий. Перевіряючи на зайвину по черзі всі складники ДНФ та їх сполучення, можна дістати мінімізовану функцію. Але такі обчислення та порівняння варіантів займають багато часу, тому цей процес також потребує формалізації.