Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 8

Діаграма для більшої кількості функцій утворюється таким чином, щоб фігура наступної функції поділяла всі ділянки попередньої діаграми на дві частини. Так, для трьох змінних (рис. 2.4,ж) прямокутник y3 перетинає всі ділянки попередньої діаграми на рис.2.4,б, а фігура y4 (рис. 2.4,з) утворює діаграму для чотирьох змінних. На останніх двох діаграмах ділянки нумеруються кодами відповідно i=y3y2y1 та i=y4y3y2y1. Нульова ділянка на цих діаграмах є доповненням диз'юнкції , а ділянка з кодом i=7 або i=15 відповідно є кон'юнкція, тобто перетин усіх функцій. Проте зміст кожної ділянки легко визначається її кодом. Так, п'ята ділянка на цих діаграмах є виразом відповідно  та , тобто немає потреби йменувати кожну з них своєю назвою.

 Комбінуючи ділянки аналогічно діаграмі для двох функцій, можна будь-яку невідому функцію виразити через інші, вже відомі. Так, логічним підсумовуванням ділянок 4...7 на діаграмі трьох функцій дістанемо пряму функцію y3, а ділянок 0...3 – інверсну функцію . Проте процедуру розв'язання логічного рівняння з багатьма функціями доцільно спростити, позначивши шукану функцію як y2, а деяку композицію попередьо синтезованих k функцій як y1, наприклад, y1=y01+y02+...+y0k або y1=y01y02y03... і т. ін. Тоді задача зводиться до діаграми на рис. 2.4,б та розв'язку за (2.6)...(2.12) за умови y1¹1. У противному разі добирається інша композиція функцій y0i, коли ця умова виконується.

На завершення звернімо ще раз увагу на нумерацію ділянок діаграм на     рис. 2.4,б,ж,з – клітинок з кодами i. Сусідніми називатимемо клітинки, розташовані поруч по горизонталі й вертикалі (але не по діагоналі). При наведеній нумерації сусідні геометрично клітинки відповідають і сусіднім кодовим наборам (коди відрізняються лише одним розрядом). Тому сусідніми на рис. 2.4,з є й крайні по горизонталі або по вертикалі, а також кутові клітинки. Отже, діаграму можна уявити як розгортку торуватої поверхні: з'єднанням верхньої і нижньої її ліній утворюється циліндр, а з'єднанням ще лівої та правої ліній – тор.

Таким чином, за допомогою теоретико-множинного уявлення про логічні функції досягається не лише наочна ілюстрація логічних операцій і доведення співвідношень, але й полегшується встановлення зв'язку між ними, що дає змогу виражати функції одна через одну з метою спрощення їх реалізації. Приклади на застосування співвідношень між функціями наводяться в § 2.3.

§2.2. МІНІМІЗАЦІЯ ЛОГІЧНИХ ФУНКЦІЙ

Логічне  проектування, особливо найпростіших пристроїв, можна здійснити  шляхом тотожних перетворень логічних функцій, проте навіть у нескладних випадках виникає потреба у формалізації перетворень, аби дістати оптимальні варіанти схеми, а досвід та інтуїцію використовувати лише на завершальних етапах проектування,  зокрема, під час вибору найкращого варіанту для реалізації. Формалізована процедура переходу від ДДНФ (ДКНФ) до більш короткої форми та вибору з-поміж багатьох варіантів зображення функції найкоротшої з них називається мінімізацією логічної фукції. Отже, мінімізація полягає в перетворенні від ДДНФ до мінімальної ДНФ (МДНФ) або від ДКНФ до мінімальної КНФ (МКНФ) функції.

2.2.1. Графічний метод  діаграм термів (Вайча – Карно)

1. Побудова діаграм.Серед формалізованих методів мінімізації логічних функцій найбільшого поширення набув метод за допомогою діаграм термів, де 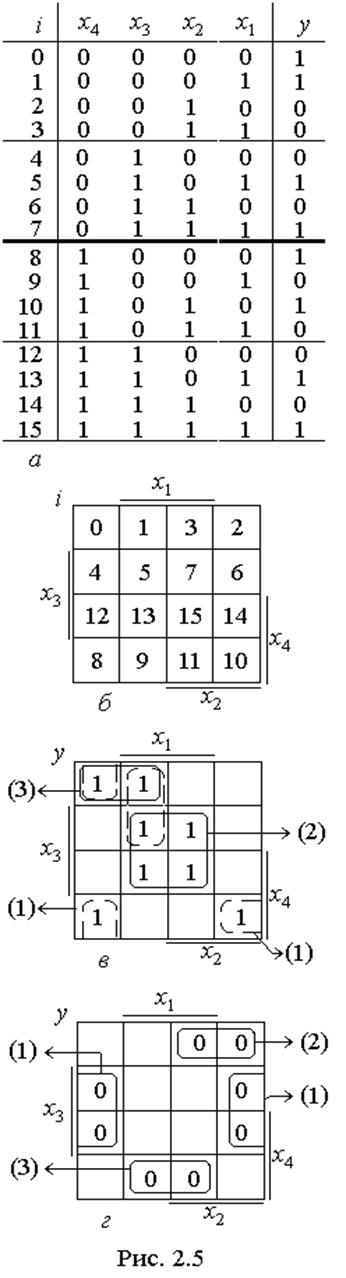як математична модель використовується діаграма, клітинки якої є терми – члени виразу ДДНФ (мінтерми) або ДКНФ (макстерми). Такі діаграми мають поширену назву діаграм Вайча або карт Карно й будуються формально так само, як і діаграми Венна або діаграми Ейлера. Для стислості називатимемо їх діаграмами термів.

Для функції yчотирьох змінних (рис. 2.5,а) клітинки діаграми термів         (рис. 2.5,б) нумеруються десятковими кодами вхідних кортежів i=x4x3x2x1 так само, як і на діаграмі Венна (див. рис. 2.4,з). Стандартна нумерація клітинок полегшує заповнення власне діаграми функції y (рис. 2.5,в). Після позначення координат рисками, що відповідають одиничним значенням змінних, до діаграми переносять лише одиниці з колонки y таблиці відповідності згідно з кодами i вхідних кортежів, а до порожніх клітинок вважаються записаними нулі, або, навпаки, переносять лише нулі (рис. 2.5,г), тоді порожні клітинки відповідають значенням y=1.