2. Схеми з кількома виходами.Порядок логічного проектування розглянемо на прикладі схеми з двома виходами y1, y2, що задана таблицею відповідності (див. рис. 2.15,а).
а) Попередньо мінімізуємо логічні функції окремо, порівнюємо їх у булевому
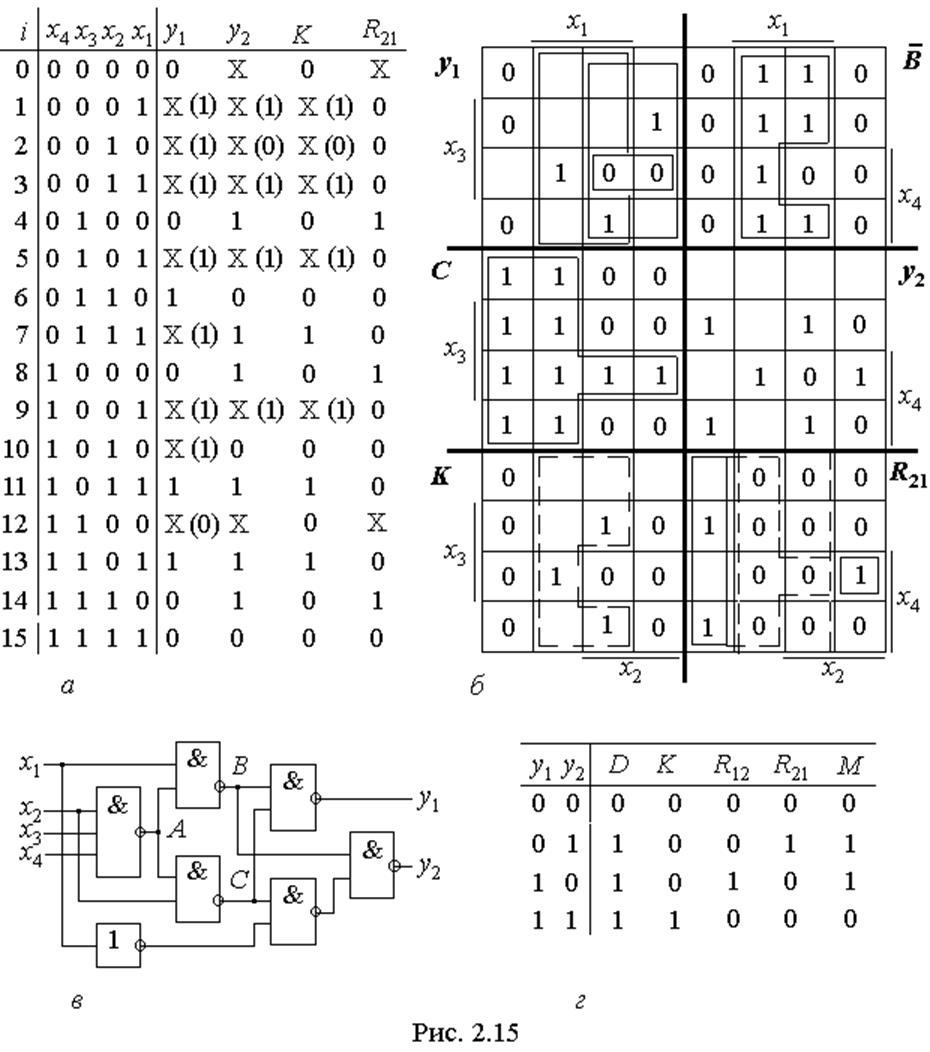
базисі та вибираємо одну з простіших, бажано таку, яка за деякими фрагментами логічного виразу або за розташуванням нулів чи одиниць на діаграмі наближається до інших. У прикладі функцію y1 визначено виразом (2.28), а функцію y2 (на діаграмах у1, у2 рис. 2.15,б подано одиниці та нулі, інші клітинки є невизначеними) мінімізуємо за сполуками одиниць та з урахуванням (2.22) зводимо до мінімальної форми
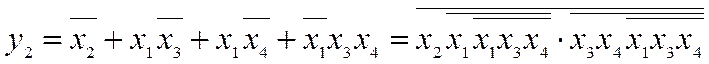(2.29)
зі складністю q=4/11. Отже, простішою вважаємо функцію y1,?? яка згідно з (2.28) складається з фрагментів A, B, C. Для наочності фрагменти B та Cподано на діаграмах рис. 2.15,б.
б) З'ясовуємо, чи не є співвідношення між шуканою функцією y2 та функцією y1, яку вважаємо відомою, окремим випадком (п.2.1.5). Безпосередньо з діаграм видно, що їх об'єднання D¹1, перетин K¹0, тому маємо загальний випадок (2.7). При реалізації схеми, наприклад, в базисі І-НЕ всі логічно еквівалентні варіанти виразу (2.7) приводять до однакового результату, тому з-поміж них слід вибрати найпростіший для мінімізації і перетворень. З порівняння діаграм у прикладі вибираємо пару K і R21 (див. рис. 2.15,б).
в) За діаграмами мінімізуємо вирази результатів вибраних операцій.
Особливістю спільної мінімізації частково визначених функцій є необхідність забезпечення сумісності операцій як між собою, так і з функціями, над якими вони виконуються, бо під час довизначення порожніх клітинок на діаграмах можуть утворитися неможливі співвідношення, що суперечать таблиці відповідності (рис. 2.15, г).
Аби уникнути цього, доцільно діяти в такому порядку. Вважаємо спочатку функцію y1 відомою і повністю визначеною (нагадаємо, що тепер порожні клітинки на її діаграмі, крім і=12, відповідають лог. 1), а функцію y2 – частково визначеною (основний її стовпець у таблиці). До стовпця перетину K=y1y2 переносимо всі нулі із зазначених колонок y1 і y2 та лише ті одиниці, що збігаються в порівнюваних стовпцях, а комбінації K=y1y2=1Х=Х залишаються невизначеними. Відтак заповнюємо діаграму К та довизначаємо порожні клітинки для утворення найкращих об'єднань.
Метою мінімізації є утворення найпростішої функції з
використанням відомих функцій або їх частин. Якщо на діаграмі K клітинку
i=2 довизначити нулем, а інші одиницями (подано в дужках біля стовпця К
таблиці), то повністю повторюється діаграма 
,
тобто
(2.30)
Цього висновку можна дійти й аналітично. Три сполуки з чотирьох одиниць кожна, зважаючи на (2.28), дають вираз
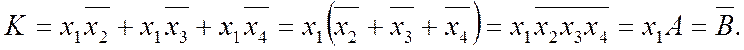
Таким довизначенням кон'юнкції автоматично довизначається й частина функції y2 (наведено в дужках біля її стовпця таблиці): y2=K, якщо y1=1, а на наборах i=0 та 12, що відповідають y1=K=0, вона лишається невизначеною.
У такий самий спосіб мінімізуємо й результат другої операції R21=y2\y1. До стовпця R21 переносимо з колонки y2 тільки ті одиниці, що відповідають y1=0, а інші значення виявляються нульовими, крім тих, де y2=Х, y1=0, які залишаються невизначеними (для і=0 та 12). Якщо довизначити їх одиницями на діаграмі R21, отримаємо діаграму C, з якої вирізано смугу одиниць завширшки x1, тобто
(2.31)
Аналітично це можна виразити з двох сполук одиниць з урахуванням (2.28):
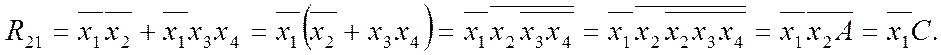
Тепер решту значень Х у стовпцях R21 та y2 довизначено до Х=1.
Таким чином, довизначаємо й мінімізуємо не саму функцію y2, а співвідношення між функціями, у нашому випадку K та R21. Якщо для спрощення виразів цих операцій бажано інакше довизначити функцію y1 без істотного її ускладнення, розглядаємо варіанти і вибираємо найкращий.
г) Завершуємо проектування аналогічно схемі з одним виходом. У прикладі згідно з (2.7), (2.30), (2.31) дістаємо структурну функцію
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.