Логічні основи цифрової техніки (Глава 2 навчального посібника), страница 3

Проте й ця система є надлишкова: вона лишається повною й у  тому разі, якщо вилучити з неї один з елементів, крім НЕ. Мінімально повною є система, з якої не можна вилучити жодної функції без утрати її повноти. Можна утворити функціонально повні системи, у тому числі й мінімальні, з різних наборів функцій, але обов’язково в них має бути інверсія. Практичного значення крім булевого  набули базиси з двох елементів: 1) І, НЕ та 2) АБО, НЕ, а частіше навіть з одного елемента: 1) І-НЕ та 2) АБО-НЕ; через це елементи  І-НЕ та АБО-НЕ називають універсальними. Проте для зменшення кількості елементів, необхідних для побудови пристрою, забезпечення гнучкості проектування використовують і складніші функції.

Отже, алгебра логіки оперує з логічними або двійковими змінними й функціями, які можуть набувати двох значень: 0 або 1. Перетворення в алгебрі логіки з метою аналізу, синтезу, доведення положень тощо здійснюють, користуючись, головним чином, основними логічними функціями НЕ, АБО, І, але під час практичної реалізації цифрових пристроїв широко застосовують елементи, що виконують комбіновані функції І-НЕ, АБО-НЕ,  І-АБО-НЕ, виключне АБО тощо.

2.1.3. Співвідношення алгебри логіки

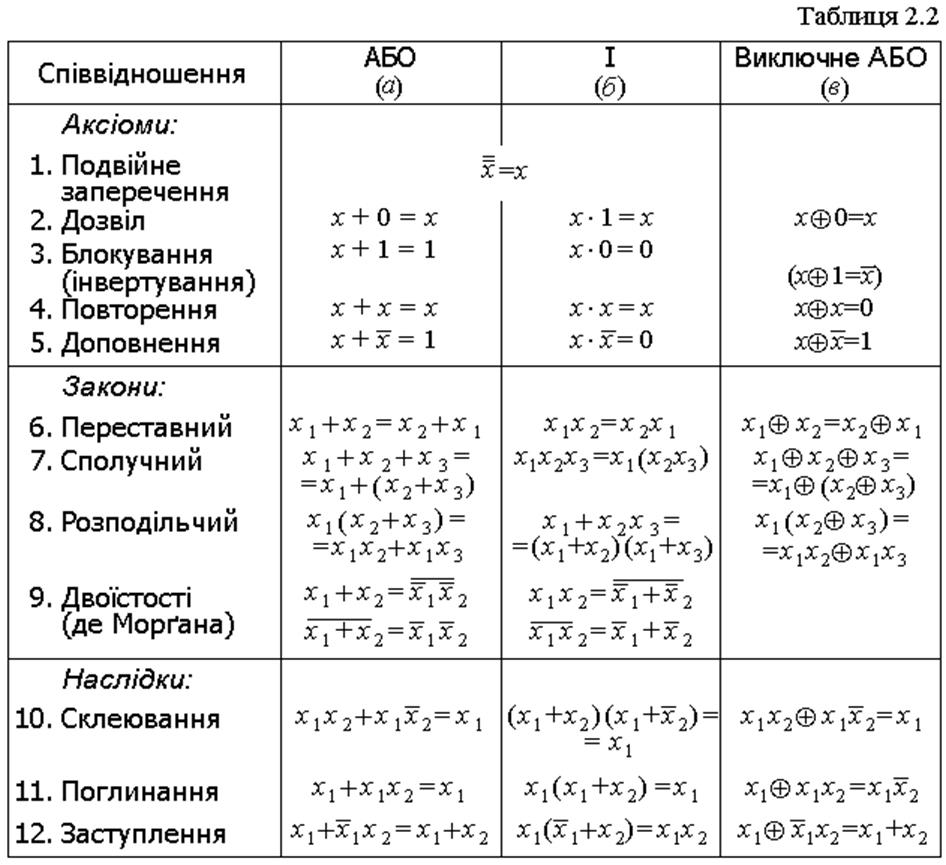
Основні співвідношення (у літературі існують також їх назви: аксіоми або тотожності, закони або теореми, наслідки законів або правила) розглядаються в булевій алгебрі, здебільшого, відносно функцій АБО та І, а справедливість тих чи тих формул відносно інших функцій з'ясовується окремо. У табл. 2.2 формули пронумеровано цифрами, що відповідають назвам співвідношень, і літерами а, б для функцій АБО та І, а з літерою в для прикладу наведено аналогічні співвідношення для функції виключне АБО.

1. Аксіоми 1...5 безпосередньо випливають із таблиць відповідності основних функцій і часто застосовуються в практиці (на рис. 2.1 нумерація формул зазначена над рисунками в дужках).

Подвійне заперечення 1 використовується для відновлення змінної х, наприклад, у схемах збільшення коефіцієнта розгалуження (рис. 2.1,а) за недостатньої навантажівної здатності елемента. На рис. 2.1,б,в,г наведено принципи побудови інверторів за допомогою аксіом; ті ж самі принципи застосовуються й для підімкнення зайвих входів мікросхем (підімкнення за аксіомами 2а,б менше навантажує джерело сигналу).

Крім того, у мікропроцесорах аксіоми застосовуються для програмованої зміни слова або окремих його бітів (на рис. 2.1,д у дужках зазначено, яка операція має міститись для цього в коді відповідної команди). У наведеному прикладі у вихідному слові 962/10, розряди якого підлягають зміні, за допомогою дібраного з цією метою другого операнда 0F16 (його вводять до складу команди) можна встановити одиниці в молодшій тетраді без зміни старшої виконанням  операції АБО, обнулити старшу тетраду без зміни молодшої виконанням операції І та зінвертувати розряди молодшої тетради без зміни старшої операцією виключне АБО.

Дозвіл або блокування проходження змінної на підставі аксіом 2а,б і 3а,б широко використовується для синхронізації пристроїв  (рис. 2.1,е). Для блокування змінних х1, х2 на спільних входах елементів АБО-НЕ встановлюють рівень лог. 1, а елеметів І-НЕ – лог. 0.  Тоді, незалежно від сигналів на інформаційних входах х1, х2 на виходах елементів буде постійний рівень відповідно   лог. 0 та лог. 1. З надходженням активного рівня синхросигналу відповідно =0 або  С=1 змінні х1, х2 з’являються на виходах (з інверсією).

2. Закони.В алгебрі логіки широко використовуються чотири закони 6...9 щодо виконання логічних операцій. Переставний закон 6 свідчить  про рівнозначність інформаційних входів логічних елементів АБО,  І, виключне АБО. Проте, природно, закон не виконується для елементів заборони та імплікатора, бо один з їх входів інверсний і  його позначення має чітко відрізнятися від прямого. Сполучний  закон 7 використовується з метою розширення кількості змінних в операціях АБО, І, виключне АБО шляхом драбинчастого каскадування елементів на кшталт рис. 2.1,є, якщо в елементі бракує входів, тобто для збільшення коефіцієнта об’єднання входів.