Складніші, комбіновані функції, зображені в булевому базисі, можна здобути шляхом сполучення елементів НЕ, І, АБО, реалізованих у базисі І-НЕ, та наступним вилученням послідовно ввімкнених інверторів (якщо вони є) за аксіомою подвійного заперечення. Так, з’єднанням двох елементів І зі входами елемента АБО (рис. 2.10,д) та вилученням двох пар послідовно ввімкнених елементів НЕ одержуємо схему, еквівалентну елементові І-АБО (рис. 2.10,е), а додаванням на виході інвертора – схему І-АБО-НЕ (рис. 2.10,є). Використовуючи елементи НЕ та І-АБО, переходимо так само від схеми виняткове АБО в булевому базисі (див. рис. 2.9,а) до схеми в базисі І-НЕ (рис. 2.10,ж).
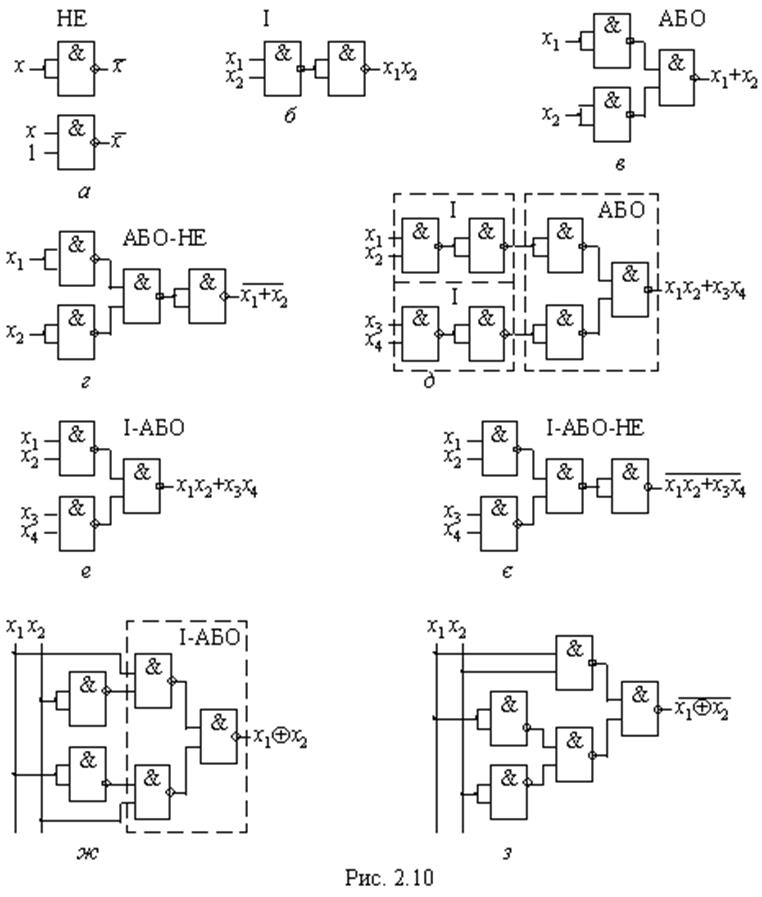
Проте реалізацію в базисі І-НЕ звичайно виконують не перетворенням схем, а алгебрично, за формулою:
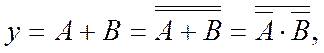(2.16)
де А, В – кон’юнкції літералів (змінних або їх заперечень). Тобто для такого перетворення необхідно: а) записати функцію в ДНФ (МДНФ або, якщо не підлягає мінімізації, ДДНФ), б) поставити над виразом два знаки інверсії та в) за законом двоїстості перейти від суми до добутку змінних або їх кон’юнкцій. Наприклад, для функції виняткове АБО, виходячи з ДДНФ (2.2), дістаємо структурну функцію
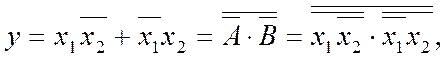
що відповідає рис. 2.10,ж.
Якщо функцію задано в КНФ, то спочатку доцільно перейти до ДНФ, а відтак – до базису І-НЕ. Наприклад, вираз (2.4) за допомогою (2.1) перетворюємо таким чином:
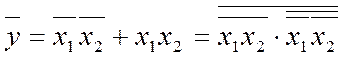
і реалізуємо елемент виняткове АБО-НЕ (рис. 2.10,з).
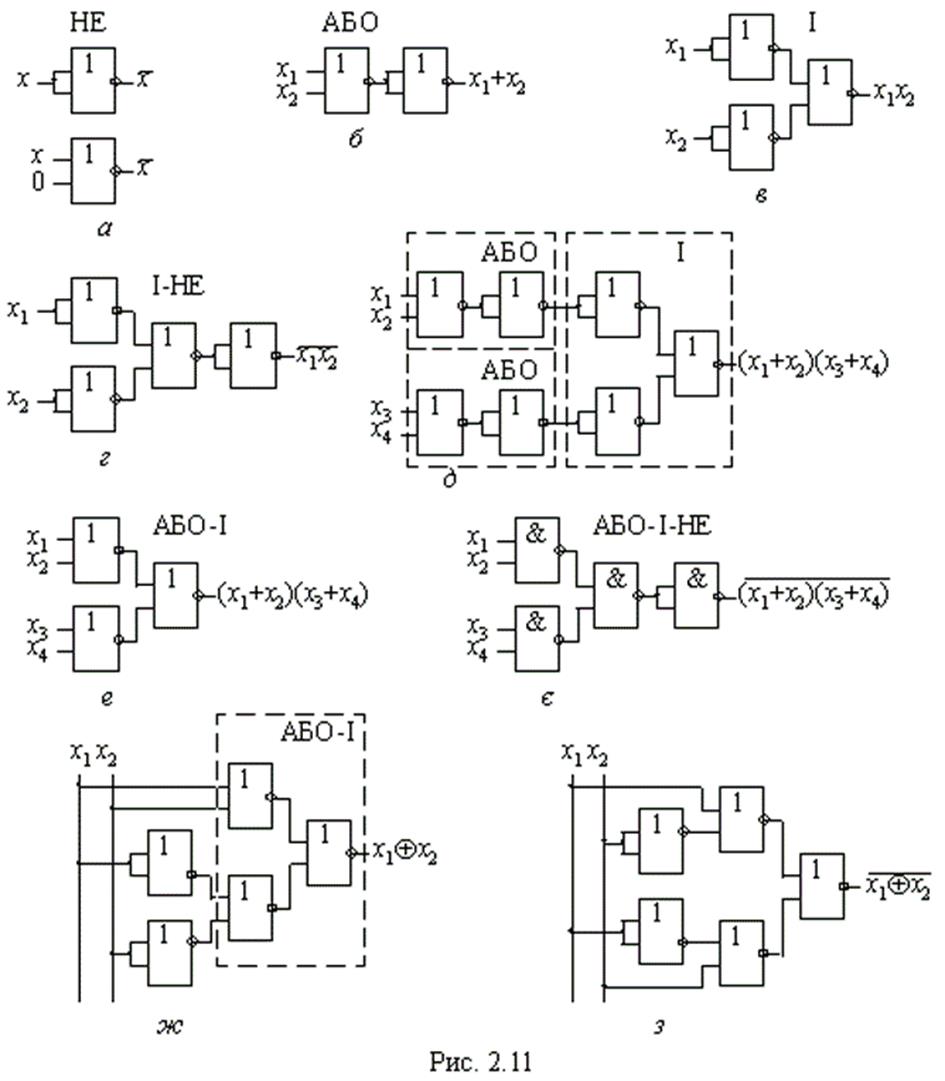
3. Базис АБО-НЕ. Реалізація логічних елементів НЕ, АБО, І, І-НЕ (рис. 2.11,а,б,в,г) та перетворення схем від булевого базису до базису АБО-НЕ шляхом заміни елементів (див. рис. 2.9,б) їх еквівалентами в базисі АБО-НЕ з усуненням пар послідовно ввімкнених інверторів, якщо вони є (рис. 2.11,д,е,є,ж), повністю дуальні перетворенням у базисі І-НЕ.
Алгебрично для переходу до базису АБО-НЕ перетворення виконують за формулою:
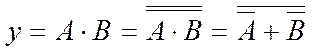(2.17)
(тут А, В – диз’юнкції літералів), тобто в такому порядку: а) записують функцію в КНФ (мінімальну, якщо вона є, інакше ДКНФ), б) позначають над виразом два знаки інверсії та в) переходять від добутку до логічної суми за законом двоїстості.
Від функції, заданої в ДНФ, попередньо згідно з (2.1) переходять до КНФ, а відтак – до базису АБО-НЕ. Наприклад, перетворенням (2.2)
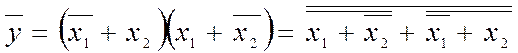
реалізується елемент виняткове АБО-НЕ (рис. 2.11,з).
4. Базис І-АБО-НЕ.Легко показати за законами двоїстості
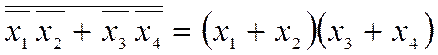
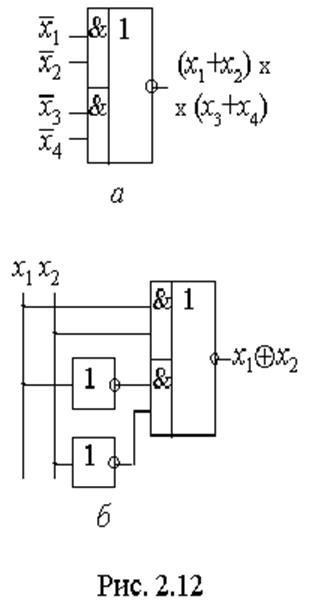
реалізацію функції АБО-І в базисі І-АБО-НЕ (рис. 2.12,а). Взагалі перетворення схем виконують алгебрично за формулами
(2.18)
тобто в послідовності: а) записують вираз інверсної функції в ДНФ та б) за допомогою інверсії над обома частинами виразу переходять до структурної функції в базисі І-АБО-НЕ.
Наприклад, з ДНФ (2.3)
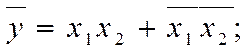
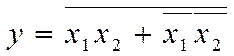
дістаємо структурну функцію, зручну для побудови елемента виняткове АБО (рис. 2.12,б).
Таким чином, вихідною для подальших перетворень з метою спрощення схеми та побудови її у потрібному базисі є мінімізована функція ДНФ або КНФ, що має зображення в булевому базисі, тобто на елементах НЕ, І, АБО. У заданому базисі функцію реалізують шляхом її алгебричного перетворення за певними правилами. При цьому до базисів І-НЕ та І-АБО-НЕ простіше перетворюються функції, зображені в ДНФ, а до базису АБО-НЕ – в КНФ.
2.3.2. Способи спрощення логічних схем
1. Проблема схемної мінімізації.Розглянута мінімізація логічної функції в МДНФ та МКНФ відображає її в булевому базисі, який є малопридатний щодо технічної реалізації. Серії сучасних інтегрованих мікросхем містять різні комплекти стандартних логічних елементів, у тому числі багатовходових, використання яких дозволяє мінімізувати схеми. Проте в загальному вигляді проблема схемної мінімізації в різних функційно повних системах на цей час не розв'язана.
У багатьох випадках мінімізація функції передує переходу від булевого до інших базисів та подальшим перетворенням з метою спрощення структурної функції.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.