Логічні основи цифрової техніки (Глава 2 навчального посібника)

Глава 2

ЛОГІЧНІ ОСНОВИ ЦИФРОВОЇ ТЕХНІКИ

§2.1. АЛГЕБРА ЛОГІКИ

2.1.1. Загальні відомості

Сукупність сигналів на входах цифрового пристрою в кожну мить часу становить певне двійкове число, а сигнал на кожному з його виходів залежить від цієї сукупності за чітко визначеними правилами. У цьому розумінні пристрій є перетворювачем цифрової інформації, його вхідні сигнали – логічними (булевими, двійковими) змінними (аргументами) хi, а вихідні – логічними (булевими, перемикальними) функціями:

yj=fj(x1,x2,...,xm).

Природно, логічні змінні та функції як підсумок виконання певної операції над ними можуть набувати в якусь мить часу одного з двох інформаційних значень: логічного 0 (лог. 0) або логічної 1 (лог. 1). З часом значення змінних, а, отже, і функцій змінюються, а якщо якийсь біт інформації, наприклад, на вході хi залишається весь час сталим, його називають константою нуля або одиниці і позначають часто знаком тотожності: хiє0 або хiє1. Якщо в двох змінних значення змінюються майже одночасно й вони завжди є протилежними, тобто змінні парафазно відображають один і той самий сигнал, то одну з них називають прямою хi, а другу – інверсною .

Абстрагуючись від фізичних процесів у схемі, її елементної бази, зручно функціонування цифрових пристроїв та моделювання  інформаційних перетворень у них розглядати за допомогою двоцифрової алгебри логіки (булевої алгебри). Для цього, передусім, потрібно якимось чином визначити залежність кожного вихідного сигналу від вхідних, тобто задати його логічну функцію. Первісними є словесний і табличний способи задання функції, з яких вже можна дістати її зображення у вигляді логічного (булевого) виразу. Практично найчастіше використовується задання за допомогою таблиці відповідності (істинності, перемикальної). Зручною є така її побудова (див., наприклад,       табл. 1.10), коли кожна змінна і функція розташовані в колонку; одночасно змінні утворюють рядки – вхідні кортежі (набори вхідних змінних, слова вхідної абетки), які є їх двійковими відповідниками. Якщо змінні розташувати в природному порядку, як і двійкові числа – від старшого розряду числа до молодшого, вони займатимуть стале положення незалежно від їх  кількості  на графічній моделі – діаграмі, що зручно під час синтезу функцій. Крім того, літерою і часто позначатимемо десятковий код вхідного кортежу для зручності посилань.

З усіх k=2m кортежів – можливих наборів змінних від 0 до 2m-1  (де m – кількість змінних) – можна утворити 2k різних функцій. Деякі з них є виродженими – це константи нуля чи одиниці і такі, що повторюють одну із  змінних або функцію від меншої кількості аргументів, а деякі не є самостійними, якщо відрізняються лише порядком розташування змінних. Тому далі розглядаються лише дві функції однієї змінної (одномісні операції) та 4 пари оригінальних функцій двох змінних (двомісні або бінарні операції); до трьох з цих пар зводяться функції і більшої кількості аргументів. Тут і далі користуватимемося, здебільшого, лаконічними термінами алгебри логіки, а паралельні назви – літературні варіанти – подаватимемо в дужках.

2.1.2. Основні логічні функції

1. Означення. У табл. 2.1 усі функції (у дужках англійською мовою зазначено їх скорочені назви, що використовуються під час програмування) подано парами: у лівих вихідних колонках таблиці відповідності та умовних графічних позначень наведено пряму функцію y0, а в правих – інверсну y1.

Лише одна з наведенних операцій – функція повторення (теж, твердження) у0=х1 (читається: як х1) є тривіальна, проте повторювач або буферний підсилювач, що її виконує, часто використовується для підвищення навантажівної здатності цифрових пристроїв та сполучення їх із шинами. Друга одномісна операція – функція НЕ (логічне заперечення, інверсія, доповнення) означає обернення аргументу х1, тобто зміну його логічного значення на протилежне. Інверсія позначається у формулах рискою над змінними: у1= (читається: не х1), а на умовних графічних позначеннях інвертора (елемента НЕ) і інших елементів – маленьким колом.

Функція АБО (логічне додавання, логічна сума, диз’юнкція, об'єднання) – це операція збирання інформації від кількох джерел до одного каналу: на виході у0 з’являється рівень лог. 1, якщо він надходить хоча б з одного з входів. Логічне додавання відрізняється від арифметичного останнім рядком таблиці: 1+1=1, позначається у0=x1+x2= (читається: x1 або x2), реалізується елементом АБО (елементом збирання, диз’юнктором). З інверсією на виході утворюється функція АБО-НЕ (логічне додавання із запереченням, стрілка Пірса, заперечення диз’юнкції, доповнення об'єднання):   у1= = 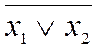(читається: ні x1, ані x2), виконується елементом АБО-НЕ (елементом Пірса).

                                                                                                              Таблиця 2.1