Частотно-избирательные системы. Длинные линии (8-9 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева)

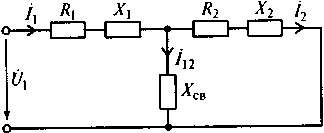
                              Рис. 7.21. Эквивалентная схема свя­занных контуров

1. Каким образом производит­ся настройка связанных конту­ров для получения максималь­ного значения тока во втором контуре при возбуждении коле­баний в первом контуре?

2. Каким образом производит­ся настройка связанных конту­ров для получения требуемой

передаточной характеристики и избирательности системы конту­ров?

Для ответа на эти вопросы сведем для примера связанные кон- 1 туры с внутренней емкостной связью (см. рис. 7.20, г) к эквива­лентной схеме связанных контуров (рис. 7.21).

Эквивалентная схема связанных контуров включает:

активное сопротивление R₁ являющееся суммой сопротивле­ний потерь элементов, входящих в первый контур, и внутреннего сопротивления источника напряжения;

реактивное сопротивление X₁, являющееся реактивным сопро­тивлением элементов первого контура;

активное сопротивление R₂, являющееся сопротивлением по­терь всех элементов второго контура;

реактивное сопротивление Х₂, являющееся реактивным сопро­тивлением всех элементов второго контура;

реактивное сопротивление элемента связи Х_св.

В соответствии с эквивалентной схемой можно записать систе­му уравнений, объединяющих токи первого I₁, и второго I₂ кон­туров, напряжения источника сигнала U₁,  активные R₁, R₂и ре­активные X₁, X₂сопротивления первого и второго контуров, а также реактивное сопротивление элемента связи Х_св:

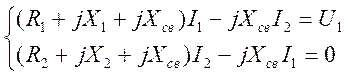
Решая систему уравнений, имеем

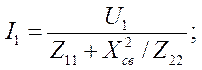
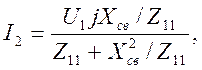
где Z₁₁ = R₁ + j(X₁ + X_св) и Z₂₂ = R₂ + j(X₂ + Х_св) -комплексные сопротивления первого и второго контуров. Сопротивления Х²_св/Z₂₂ = Z_внl и Х²_св/Z₂₂ = Z_вн2 можно рассматривать как вноси­мые сопротивления. При этом Z_внl характеризует влияние второго контура на процессы, происходящие в первом контуре, a Z_вн2 — влияние первого контура на процессы во втором контуре.

С учетом внесенных сопротивлений Z_внl и Z_вн2 связанные конту­ры можно представить двумя самостоятельными контурами (рис. 7.22) со своими источниками энергии Е₁= U₁, и E₂ = U₁jX₁₂/Z₁₁ , па­раметрами исходных контуров Х_1к = X1 + Х_св и

Х_2к = Х2 + Х_св.

Разбиение связанных контуров на две самостоятельные эквива­лентные схемы первого (см. рис. 7.22, а) и второго (см. рис. 7.22, б) контуров позволяет рассмотреть различные варианты настройки связанных контуров: на первый и второй частные резонансы; на сложный и полный резонансы.

При настройке на первый частный резонанс стремятся полу­чить максимальный ток первого контура на резонансной частоте. Достигается это при условии, что реактивное сопротивление пер­вого контура Х_1к = X₁ + Х_свравно реактивному сопротивлению, внесенному в первый контур и взятому с противоположным зна­ком: Х_1к = -X_вн1. Таким образом, при настройке на первый частный резонанс достигается равенство нулю на резонансной частоте сум­мы всех реактивных сопротивлений, входящих в первый контур.

При настройке на второй частный резонанс стремятся к полу­чению максимального тока второго контура. Достигается это под­бором составляющих реактивных сопротивлений второго контура таким образом, чтобы Х_2к = -Х_вн2. Последнее соответствует равен­ству нулю суммы реактивных сопротивлений второго контура на резонансной частоте.

При настройке на сложный резонанс первый и второй конту­ры предварительно настраивают на частные резонансы, а затем выбирают оптимальное сопротивление элемента связи Х_св. В этом случае достигается максимум максимумов тока второго контура

                                                                (7.19)

Соответственно при настройке на сложный резонанс стремят­ся к выполнению условий Z₁₁ = Z_вн1, и Z₂₂= Z_вн1 относительно ком­плексных сопротивлений первого и второго контуров.

При настройке на полный резонанс осуществляется настройка первого и второго контуров на частные резонансы Х_1к = 0 и Х_2к = 0, а затем выбирается оптимальная связь между контурам

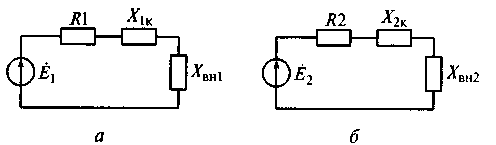
рис. 7.22. Эквивалентные схемы первого (а) и второго (б) контуров свя­занного колебательного контура

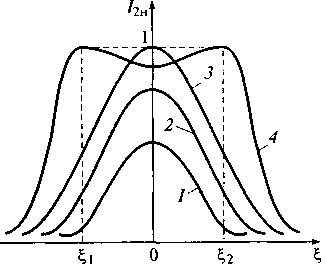
                                 Рис. 7.23. АЧХ связанных контуров

         В этом случае ток второго кон­тура будет определяться выраже­нием (7.19).

Сравнение настроек на слож­ный и полный резонансы пока­зывает, что во втором случае ток I_{2max max} достигается при меньшем сопротивлении связи.

Применительно к связанным контурам важным является за­висимость тока I₂ или нормиро­ванной величины тока I_2н = I₂/ I_{2max max} второго контора от частоты.

При слабой связи между пер­вым и вторым контурами вид АЧХ связанных контуров (рис. 7.23) аналогичен АЧХ одиночного колебательного контура. Максимум I_2н достигается при  = 0 (кривые 1, 2 и 3 на рис. 7.23). Наконец, при сильной связи АЧХ связанных контуров становится двугор­бой (кривая 4 на рис. 7.23). При  = 0 значение I_2н становится меньше единицы, а при  и  значение I_2н достигает максимума I_2н = 1.        Частоты, на которых достигаются максимумы I_2н, при  соответственно равны:  и . С уве­личением связи между контурами (величина k_св растет при постоян­ной добротности Q) частота  уменьшается, а частота  возра­стает.

ГЛАВА 8

ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ СИСТЕМЫ

8.1. Основные понятия и определения фильтрующих устройств

Электрический фильтр — это один или множество четырехпо­люсников, соединенных между собой, пропускающих электри­ческие колебания в определенном диапазоне частот и ослабляю­щих колебания вне этого диапазона частот. Полоса (полосы) час­тот, в которой электрические колебания проходят через фильтр практически без ослабления, называется полосой пропускания или полосой прозрачности фильтра. Полоса (полосы) частот, в которой электрические колебания ослабляются, называется полосой задер­жания или полосой непрозрачности фильтра.

По диапазонам частот прозрачности и непрозрачности фильтры разделяют на следующие виды (рис. 8.1):

фильтры нижних частот (ФНЧ), для которых диапазон частот прозрачности простирается от = 0 до некоторой частоты среза и = _ср = 2πf_ср фильтра, а диапазон частот непрозрачности — от  = _ср до  = . На рис. 8.1, а представлена АЧХ идеального ФНЧ.

фильтры верхних частот (ФВЧ), для которых диапазон частот непрозрачности простирается от  = 0 до  = _ср, а диапазон частот прозрачности — от  = _ср до  =  (см. рис. 8.1, б);

полосовые фильтры (ПФ), для которых диапазон частот про­зрачности простирается от  = _ср1, до  = _ср2, а диапазон частот непрозрачности — от  = 0 до  = _cpl и от частоты  = _ср2 до  =  (см. рис. 8.1, в), где _ср1 и _ср2 — первая и вторая частоты среза фильтра;

режекторные (заградительные) фильтры (РФ), для которых ди­апазон частот прозрачности простирается от  = 0 до  = _ср1, и от  = _ср2 до  = , а диапазон частот непрозрачности — от  = _ср1, до  = _ср2 (см. рис. 8.1, г).

Амплитудно-частотные характеристики, представленные на рис. 8.1, соответствуют идеальным фильтрам, в которых переход из области прозрачности в область непрозрачности происходит практически скачкообразно. В реальных же фильтрах этот переход занимает определенный диапазон частот _ср-₃, где ₃ — частота запаздывания. Чем уже диапазон частот перехода фильтра из обла­сти прозрачности в область непрозрачности, тем лучше характе­ристики фильтра. Однако построение подобных фильтров требует использования большого числа элементов.