 |
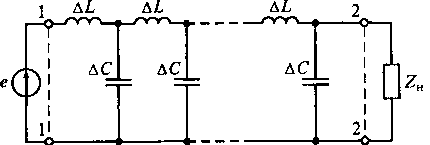
Рис. 9.3. Схема замещения идеальной длинной линии
Реальные длинные линии конструируются так,
чтобы параметры R0 и G0, обусловливающие потери в них, были как можно меньше. В этом
случае на высоких частотах достаточно хорошо выполняются соотношения R0<<![]() L0 и G0<<
L0 и G0<<![]() C0. Это позволяет в соответствующем частотном
диапазоне пренебречь потерями и полагать R0=
0 и G0=0. Линия без потерь называется идеальной длинной линией. Схема
замещения идеальной длинной линии существенно упрощается и принимает вид,
приведенный на рис. 9.3.
C0. Это позволяет в соответствующем частотном
диапазоне пренебречь потерями и полагать R0=
0 и G0=0. Линия без потерь называется идеальной длинной линией. Схема
замещения идеальной длинной линии существенно упрощается и принимает вид,
приведенный на рис. 9.3.
С математической точки зрения анализировать электромагнитные процессы в идеальной линии гораздо легче, чем в линии с потерями. При этом, как показывают результаты точного анализа, учет небольших по величине потерь в линии существенно не меняет выводов, относящихся к идеальной линии.
Схема замещения на рис. 9.3 позволяет
рассматривать идеальную двухпроводную линию как ФНЧ с числом звеньев n, определяемым целой частью числа 1/![]() х. Схема замещения идеальной линии
может быть представлена как последовательное соединение элементарных
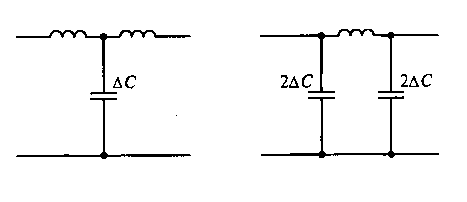
низкочастотных звеньев. На рис. 9.4 показаны схемы звеньев Т- и П-типа схемы
замещения идеальной линии.
х. Схема замещения идеальной линии
может быть представлена как последовательное соединение элементарных
низкочастотных звеньев. На рис. 9.4 показаны схемы звеньев Т- и П-типа схемы
замещения идеальной линии.
 |
а б
Рис. 9.4. Схемы звеньев Т- (а) и П-типа (б) схемы
замещения идеальной линии
Каждое звено многозвенного ФНЧ
эквивалентно участку линии длиной Ах с параметрами ![]() и
и
![]() .
.
Используя модель Т- или П-типа, можно определить характеристическое сопротивление р схемы замещения идеальной длинной линии на нулевой частоте :
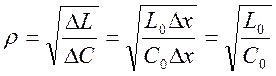
В теории цепей с распределенными
параметрами величину ![]() называют волновым
сопротивлением идеальной длинной линии. Волновое сопротивление линии без
потерь чисто активно и не зависит от частоты. Сопротивление W относится к группе вторичных параметров
линии и играет важную роль при анализе режимов ее работы.
называют волновым
сопротивлением идеальной длинной линии. Волновое сопротивление линии без
потерь чисто активно и не зависит от частоты. Сопротивление W относится к группе вторичных параметров
линии и играет важную роль при анализе режимов ее работы.
9.3. Волновые процессы в идеальной длинной линии
Прежде чем приступить к анализу волновых процессов в реальной длинной линии, рассмотрим сущность процессов в идеальной линии.
Фазовая скорость волны. Всякий волновой периодический процесс можно характеризовать понятием фазы волны. Любая физическая величина, участвующая в таком процессе, периодически изменяется в определенном интервале значений. Состояние волнового процесса, соответствующее конкретному значению переменной величины из этого интервала, и называется фазой волны. Так как фаза в данном случае характеризует периодический процесс, то и сама она является периодической функцией. Это означает, что состояние волны периодически повторяется при движении ее в пространстве и изменении во времени.
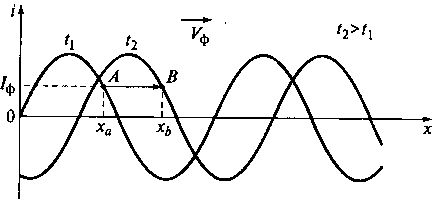 |
Рис. 9.5. Графики распределения тока в гармонической волне
Для понимания сущности фазовой скорости
волны рассмотрим рис. 9.5, на котором представлены графики распределения тока в гармонической волне вдоль линии передачи для двух
моментов времени t1 и t2 (t2> t1). На рисунке точкой А обозначено
значение тока IФ в
некоторой фазе, соответствующей моменту времени t1и координате
ха (волна распространяется в положительном направлении оси
Ох). При распространении волны фазовая точка А перемещается в положение
В на расстояние ![]() х = ха - хь
за время
х = ха - хь
за время ![]() t = t2 – t1. При этом положение
фазовой точки В относительно других фазовых состояний в волне для
момента времени t2 такое
же, что и точки А в момент t1. Это
означает, что фазы волны в точках А и В совпадают. Таким образом,
чтобы проследить за перемещением волны, достаточно проследить за перемещением
какой-либо ее точки с конкретной и неизменной фазой. Скорость такого
перемещения называется фазовой скоростью волны. За период колебаний T
волна распространяется на расстояние, равное ее длине
t = t2 – t1. При этом положение
фазовой точки В относительно других фазовых состояний в волне для
момента времени t2 такое
же, что и точки А в момент t1. Это
означает, что фазы волны в точках А и В совпадают. Таким образом,
чтобы проследить за перемещением волны, достаточно проследить за перемещением
какой-либо ее точки с конкретной и неизменной фазой. Скорость такого
перемещения называется фазовой скоростью волны. За период колебаний T
волна распространяется на расстояние, равное ее длине ![]() .
.
Если электромагнитная волна распространяется в неограниченной
диэлектрической среде с относительными диэлектрической ![]() и
магнитной
и
магнитной ![]() проницаемостями, то ее фазовая
скорость vфравна скорости света в данной среде.
проницаемостями, то ее фазовая
скорость vфравна скорости света в данной среде.
При распространении волны в длинной линии ее фазовая
скорость зависит от структуры волны в линии (от пространственной ориентации
векторов ![]() и
и ![]() в
волне) и может быть как больше, так и меньше скорости света. В частности, в
двухпроводной линии фазовая скорость волны равна фазовой скорости света в
изолирующей среде, в которой находятся проводники линии.
в
волне) и может быть как больше, так и меньше скорости света. В частности, в
двухпроводной линии фазовая скорость волны равна фазовой скорости света в
изолирующей среде, в которой находятся проводники линии.
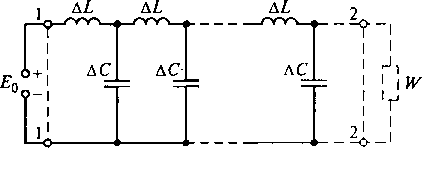
Идеальная линия с источником постоянного напряжения. Рассмотрим схему замещения бесконечной идеальной длинной линии (рис. 9.6), к входу которой подключен источник постоянного напряжения Е0.
Бесконечно длинная линия реально не существует и представляет собой идеализированный объект. В такой линии поток электромагнитной энергии распространяется только в одном направлении: от источника сигнала к противоположному концу линии, удаленному на бесконечность. Такой однонаправленный характер распространения энергии существует и в реальной линии конечной длины, нагруженной на активное сопротивление, равное волновому сопротивлению W.
 |
12 т ![]()
![]()
Рис. 9.6. Схема замещения бесконечной идеальной длинной линии
На рис. 9.6 целые числа внизу под схемой замещения
соответствуют порядковому номеру соответствующего элементарного участка линии
длиной ![]() х. Каждое элементарное звено схемы
замещения нагружено на такое же последующее звено, и так как линия бесконечна,
то каждое звено нагружено на свое характеристическое сопротивление, равное
волновому сопротивлению линии W.
х. Каждое элементарное звено схемы
замещения нагружено на такое же последующее звено, и так как линия бесконечна,
то каждое звено нагружено на свое характеристическое сопротивление, равное
волновому сопротивлению линии W.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.