Частотно-избирательные системы. Длинные линии (8-9 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 11

Наличие бегущей волны в линии означает, что в ней запасает­ся энергия электромагнитного поля. На единичном отрезке линии запасается энергия электрического поля  и энергия маг­нитного поля . Мощность, отдаваемая источником напряжения в линию, Р =E₀i₀. В соответствии с законом сохранения энергии в идеальной длинной линии мощность источника долж­на быть равна энергии, запасаемой в электромагнитном поле ли­нии за одну секунду, т.е.

                                               

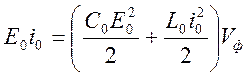
Влияние сопротивления нагрузки на волновые процессы в ли­нии. Установлено, что в однородной бесконечной идеальной дли­ной линии волновой процесс возможен только в форме бегущей волны, распространяющейся от источника вдоль линии. Поток электромагнитной энергии, переносимый этой волной, распрос­траняется в том же направлении.

Реальные линии передачи всегда имеют конечную длину и на­гружены на конце в общем случае на комплексное сопротивление нагрузки Z_H, не равное волновому сопротивлению линии W. В этом случае, как следует из условия согласования источника с нагруз­кой, не вся мощность, отдаваемая источником в линию и пере­носимая падающей волной, будет поглощена нагрузкой. Наличие избытка мощности в линии приводит к возникновению отражен­ной бегущей волны, распространяющейся от нагрузки к началу линии и переносящей в том же направлении эту избыточную мощ­ность.

При наличии одновременно падающей и отраженной волн характер электромагнитных процессов в линии усложняется. Рас­смотрим для примера однородную идеальную линию, нагружен­ную на активное сопротивление R_H>W. Пусть волновое сопротив­ление линии W = 75 Ом, сопротивление нагрузки R_H = 150 Ом и напряжение генератора E₀ = 75 В. Тогда ток в падающей волне i₀ =E₀/W=1 А. Ток в нагрузке при напряжении на ней и_н= E₀= 75 В i_н0= E₀/R_H= 0,5 А. Это означает, что при достижении волновым фронтом нагрузки напряжение и_н на сопротивлении R_H начнет повышаться и в некоторый момент превысит значение E₀, так как i₀> i_н0. В результате через конечную элементарную емкость линии потечет дополнительный ток i_доп, который подзарядит ее до на­пряжения большего, чем E₀. От этой емкости зарядится предпос­ледняя емкость и т.д. Таким образом, в линии в направлении от нагрузки к источнику возникнет отраженная волна. На рис. 9.9 показана схема процесса образования отраженной волны в одно­родной идеальной линии.

В общем случае отраженная волна всегда возникает в линии при выполнении условия Z_HW.

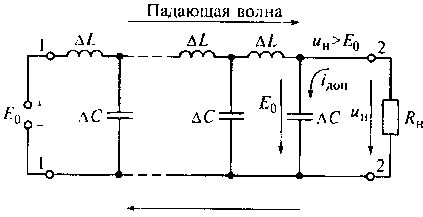Рис. 9.9. Схема процесса образования отраженной волны в однородной

идеальной линии

Интенсивность отраженной волны в линии с пассивной на­грузкой в соответствии с законом сохранения энергии может быть равна или меньше интенсивности падающей волны. В первом случае результирующий процесс в линии называется стоячей волной и не сопровождается переносом энергии вдоль линии. Во втором случае результирующая волна в линии называется смешанной вол­ной. При этом в линии осуществляется перенос энергии от источ­ника к нагрузке, однако энергия, потребляемая нагрузкой, мень­ше, чем при отсутствии отраженной волны, т.е. при Z_H= W.

Бегущая волна в нагруженной линии существует только тогда, когда падающая волна, идущая от источника, в процессе распро­странения нигде не претерпевает отражения. Для этого линия дол­жна быть однородной и сопротивление нагрузки должно быть рав­ным волновому сопротивлению линии.

Таким образом, в длинной линии в зависимости от соотноше­ния ее волнового сопротивления и сопротивления нагрузки воз­можны три волновых процесса: бегущая, смешанная или стоячая волны. В соответствии с этим различают три режима работы длин­ной линии:

режим бегущей волны (Z_H= W). От источника к нагрузке пере­дается максимально возможная мощность;

режим стоячей волны. Мощность от источника к нагрузке вдоль линии не передается;

режим смешанной волны (Z_H= W). Мощность, передаваемая от источника к нагрузке, зависит от соотношения Z_Hи W. Она мень­ше, чем в режиме бегущей волны.

Из характеристик режимов работы линии видно, что с точки зрения передачи мощности в нагрузку наиболее оптимальным является режим бегущей волны.

Идеальная линия с источником гармонического напряжения. Длин­ная линия является линейной цепью и к ней, как ко всякой ли­нейной цепи, применим принцип суперпозиции. Благодаря этому принципу, зная гармонический состав сложного сигнала, можно выявить закономерности его распространения по линии, если из­вестны закономерности распространения простого гармоничес­кого сигнала.

Для выяснения этих закономерностей рассмотрим идеальную линию длиной l, нагруженную на активное сопротивление R_H= W, к входу которой подключен генератор гармонического напряже­ния, определяемого выражением

                                                    (9.1)

где  и Т — соответственно круговая частота и период, a U_m — амплитуда гармонических колебаний напряжения на выходе гене­ратора.

Аргумент синуса  представляет собой фазу гармони­ческих колебаний напряжения. На рис. 9.10 представлены графики временной и координатной зависимости напряжения для колеба­ний на выходе генератора и для волнового процесса в длинной линии от времени для интервала времени 0  t  Т. Для удобства рассмотрения на графике отмечены пронумерованными точками девять значений напряжения, отстоящих друг от друга на равных временных интервалах t= T/8 (см. рис. 9.10, а). Под графиком на горизонтальной оси указаны фазы, соответствующие выделенным значениям напряжения.

При включении генератора на входе линии появляется в соот­ветствии с (9.1) меняющееся по гармоническому закону напря­жение. В течение каждого бесконечно малого интервала времени d/ напряжение на выходе линии можно считать постоянным. Оно будет инициировать в линии в течение этого интервала такие же процессы, как и рассмотренные ранее при подключении к линии генератора постоянного напряжения. Таким образом, каждое зна­чение напряжения, возникающее на входе идеальной линии, бу­дет распространяться вдоль нее без изменения с фазовой скорос­тью V_ф. А так как напряжение на входе линии меняется непрерыв­но по синусоидальному закону, то по такому же закону напряже­ние будет распределено по длине линии. График этого распреде­ления для момента t= T представлен на рис. 9.10, б.