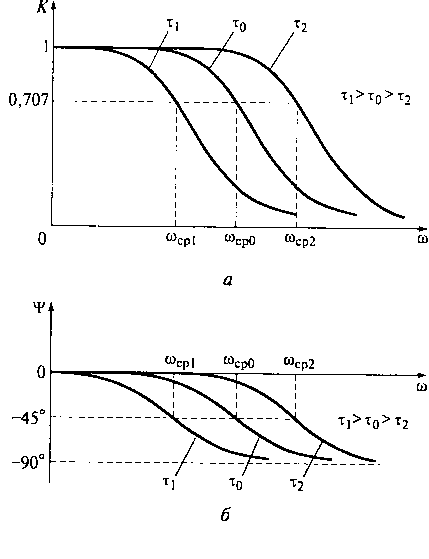Частотно-избирательные системы. Длинные линии (8-9 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 6

 

Рис. 8.14. АЧХ (а) и ФЧХ (б) ФНЧ

Комплексную частотную характеристику ФВЧ (см. рис. 8.13, б) можно представить в виде

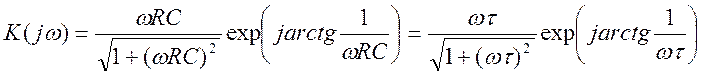
где  = RC — постоянная времени звена ФВЧ.

На рис. 8.15 приведены графики АЧХ и ФЧХ, ФВЧ, на которых

видно, что при нулевой частоте (= 0) модуль коэффициента передачи напряжения фильтром равен нулю, а аргумент 90°. По мере увеличения частоты модуль возрастает, а аргумент снижается. В пределе при частоте, стремящейся к бесконечности, модуль ко­эффициента передачи стремится к единице, а аргумент — к нулю.

Уровень 0,707 максимального значения модуля коэффициента передачи напряжения определяет частоту среза _cр звена ФВЧ. Для этой частоты выполняется условие  

_ср= 1. Отсюда можно заклю­чить, что с ростом постоянной времени звена фильтра частота среза _cр1 снижается, а при снижении  частота среза _cр2 растет. Аргумент комплексного коэффициента передачи ФВЧ при _ср= 1 равен 45°. При частоте, стремящейся к бесконечности, аргумент стремится к нулю.

 

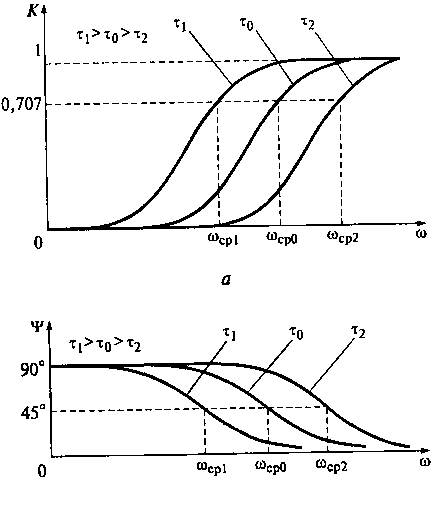Рис. 8.15. АХЧ (а) и ФЧХ (б) ФВЧ

Полосовой фильтр (см. рис. 8.13, в) RC-типа так же, как и фильтр LС-типа, позволяет выделить спектральные составляю­щие сигнала в определенном диапазоне частот _ср1ср2. Этот фильтр состоит из каскадно-соединенных ФВЧ (конденсатор С1 и резистор R1)и ФНЧ (резистор R2и конденсатор С2). Пусть для ФВЧ постоянная времени звена ₁ = L₁С₁, а для ФНЧ ₂ = L₂С₂. Тогда для работы полосового фильтра необходимо, чтобы выпол­нялось условие ₁>₂.

Частотная зависимость модуля коэффициента передачи напря­жения полосового фильтра RС-типа (см. рис. 8.13, в) показана на графике АЧХ ПФ (рис. 8.16). Для упрощения принято, что емкости конденсаторов равны между со­бой C₁ = С₂ и ₁=n₂, где п — коэффициент, определяемый от­ношением сопротивлений рези­сторов (R₁/R₂= п).

 

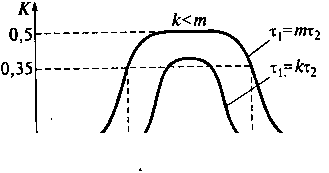
Рис. 8.16. АЧХ ПФ RС-типа

Анализируя графики на рис. 8.16, заметим следующее.                              

1. На частоте со = 0 модуль коэффициента передачи напряжения стремится к нулю.          

 

На частоте, стремящейся к бесконечности, модуль коэффициента передачи напряжения также равен нулю.

2.  Модуль коэффициента пе­редачи напряжения достигает максимального значения, когда выполняется условие = 1 . В этом случае К() = п/(2п +1). При равенстве постоянных вре­мени первого и второго звеньев фильтра  модуль коэффициента напряжения К()=1/3. При увеличении коэффициента п модуль коэффициента передачи напря­жения повышается и при п, стремящемся к бесконечности, К()= 0,5. Например, при п = 10 модуль К()= 0,476.

3.  Аргумент комплексного коэффициента передачи напряже­ния имеет сложную зависимость от частоты и коэффициента п. Так, при частоте = 0 и коэффициенте п = 1 аргумент  = 18°, а при п = 10 = 2,7°. При частоте, стремящейся к бесконечности, аргумент равен -90°, а при частоте, отвечающей условию , аргумент равен нулю.

На рис. 8.13, г для примера приведена схема режекторного фильтра, представляющего собой параллельное соединение двух фильтров. Это Т-образные звенья ФВЧ, включающего конденса­тор С1 и резистор R2, и ФНЧ, включающего резистор R1 и кон­денсатор С2. В этом случае режекторный фильтр представлен по схеме двойного Т-образного моста. Особенность этой схемы со­стоит в том, что на некоторой частоте _р токи на выходах обоих Т-образных звеньев равны между собой, но противоположны по знаку. 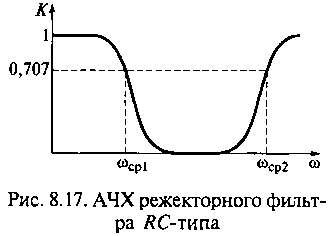Сложение этих токов приводит к тому, что ток в нагрузке равен нулю, т.е. на частоте _р коэффициент передачи напряжения режекторного фильтра равен нулю, что наглядно видно на графи­ке АЧХ режекторного фильтра RС-типа (рис. 8.17). Отклонение частоты  от частоты _р в сторону увеличения или уменьшения приводит к повышению коэффициента передачи напряжения фильтра. На этом и основана работа режекторного фильтра.

8.7. Фильтры повышенной добротности и избирательности

Однозвенные фильтры LC- и RС-типа, как правило, не отве­чают условиям избирательности, которые предъявляются к ра­диотехническим устройствам. Устранить этот недостаток и увели­чить добротность фильтров, т.е. сузить диапазон частот перехода из области прозрачности в область непрозрачности фильтра, мож­но, используя фильтры сосредоточенной селекции (ФСС).

Эти фильтры делятся на фильтры, в основе которых лежат высокодобротные колебательные контуры и различного рода резонаторные фильтры.

Одна из разновидностей ФСС — каскадное соединение высо­кодобротных контуров, в качестве элементов связи между которы­ми используют конденсаторы. Входные и выходные контуры на­гружены на резисторы, согласованные относительно характерис­тического сопротивления контуров ФСС. Добротность этих филь­тров определяется добротностью отдельных контуров и не может быть выше их добротности. К резонаторным фильтрам относят электромеханические фильтры, а также фильтры, в которых ис­пользуется магнитострикционный эффект, и фильтры, работа которых основана на использовании пьезоэлектрического эффекта.

Электромеханический фильтр состоит из преобразователя вход­ного сигнала в механические колебания, механического резона­тора и преобразователя механических колебаний в электрический сигнал. В качестве механического резонатора используют металли­ческие диски, шарики или пластинки, соединяющиеся между собой металлическими стержнями. Добротность электромехани­ческих фильтров достигает нескольких тысяч, что позволяет по­строить высокоизбирательные устройства.