Из проведенного анализа видно, что в линии возникает
волновой процесс. На участке линии, занятом волной, напряжение непрерывно
меняется вдоль нее по синусоиде. Порядок расположения пронумерованных точек на
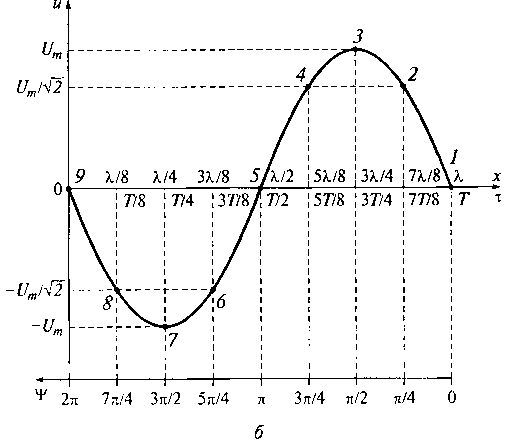
рис. 9.10, б противоположен их порядку на рис. 9.10, а. Действительно,
значения напряжения, появляющиеся на входе линии в более ранние моменты
времени, т.е. имеющие меньшие значения фазы, распространяются вдоль линии на
более дальние расстояния. За время, равное периоду колебаний Т, волна
распространится вдоль линии на расстояние, равное ее длине ![]() . На рис. 9.10, б над осью Ох
отложены расстояния, пройденные каждой точкой волны вдоль линии (на момент
рассмотрения). Под этой осью отложено соответствующее время
. На рис. 9.10, б над осью Ох
отложены расстояния, пройденные каждой точкой волны вдоль линии (на момент
рассмотрения). Под этой осью отложено соответствующее время ![]() движения этих точек. Под графиком на
рис. 9.10, о находится горизонтальная ось значений фаз для пространственно
распределенных точек волны, отсчитываемых от момента возникновения колебаний.
Эти фазы также имеют порядок расположения, обратный показанному на рис. 9.10, а.
движения этих точек. Под графиком на
рис. 9.10, о находится горизонтальная ось значений фаз для пространственно
распределенных точек волны, отсчитываемых от момента возникновения колебаний.
Эти фазы также имеют порядок расположения, обратный показанному на рис. 9.10, а.
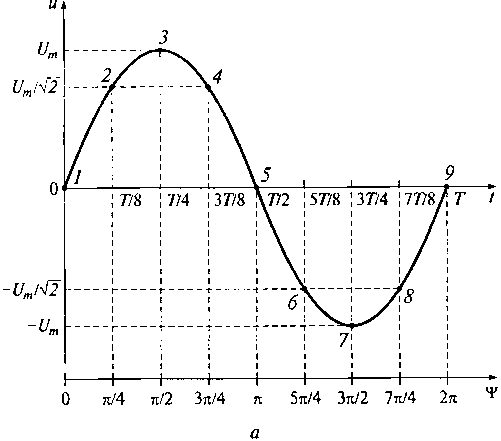 |
||
 |
||
Рис. 9.10. Временная и координатная зависимости напряжения для колебаний на выходе генератора (а) и для волнового процесса в длинной линии (б)
Заметим, что график на рис. 9.10. б отображает
закон изменения напряжения в волне вдоль длинной линии для фиксированного
момента времени. Если зафиксировать какую-либо точку в линии и проследить за
напряжением в этой точке (например, с помощью осциллографа), то увидим, что оно
будет изменяться во времени по синусоидальному закону, такому же как на выходе
генератора. Следовательно, напряжение в волне является синусоидальной функцией
координаты х и времени t и в общем виде для идеальной линии по аналогии с
выражением (9.1) может быть представлено формулой u(t)![]() где
где ![]() —
фаза волны, являющаяся функцией координат и времени.
—
фаза волны, являющаяся функцией координат и времени.
Чтобы установить явный вид функции ![]() , обратимся к пронумерованным
точкам, отмеченным на графиках рис. 9.10. Заметим, что время существования
колебаний напряжения на выходе генератора t равно
времени существования волнового процесса, возбуждаемого генератором в линии т.
Для m-й точки (т
= 1...9) волны можно указать время tmвозникновения
соответствующего значения напряжения на входе линии (выходе генератора) и
время
, обратимся к пронумерованным
точкам, отмеченным на графиках рис. 9.10. Заметим, что время существования
колебаний напряжения на выходе генератора t равно
времени существования волнового процесса, возбуждаемого генератором в линии т.
Для m-й точки (т
= 1...9) волны можно указать время tmвозникновения
соответствующего значения напряжения на входе линии (выходе генератора) и
время ![]() т распространения
этого значения напряжения вдоль линии. Из графиков на рис. 9.10 следует, что tm=
т распространения
этого значения напряжения вдоль линии. Из графиков на рис. 9.10 следует, что tm= ![]() -
- ![]() т
= t-
т
= t-![]() т. Например, для
точки с номером т = 6 имеем:
т. Например, для
точки с номером т = 6 имеем: ![]() .
.
Выражение для фазы т-й точки волны
напряжения в линии, имеющей координату хт= Vф /![]() m, можно
преобразовать к виду
m, можно
преобразовать к виду
![]()
Определим физический смысл коэффициента фазы ![]() волны в линии. Для этого рассмотрим
две точки в линии с координатами х1 и х2.
Разность фаз волны в этих точках
волны в линии. Для этого рассмотрим
две точки в линии с координатами х1 и х2.
Разность фаз волны в этих точках ![]() . Видно, что коэффициент фазы
. Видно, что коэффициент фазы ![]() численно равен разности фаз волны
на концах отрезка единичной длины, т.е.
численно равен разности фаз волны
на концах отрезка единичной длины, т.е. ![]() при
при
![]() х= 1 м. Коэффициент фазы
х= 1 м. Коэффициент фазы ![]() измеряется в 1/м.
измеряется в 1/м.
Коэффициент фазы ![]() относится
к группе вторичных параметров длинной линии. Учитывая выражение для фазовой
скорости
относится
к группе вторичных параметров длинной линии. Учитывая выражение для фазовой
скорости
![]() , получим соотношение
, получим соотношение
![]() , связывающее коэффициент фазы с
первичными параметрами линии. Таким образом, можно записать выражение
, связывающее коэффициент фазы с
первичными параметрами линии. Таким образом, можно записать выражение ![]() для фазы волны в произвольной точке
линии с координатой x.
для фазы волны в произвольной точке
линии с координатой x.
Полученная формула позволяет конкретизировать выражение для бегущей гармонической волны напряжения в линии передачи:
![]() (9.2)
(9.2)
Для идеальной линии, нагруженной на активное сопротивление RH= W, волне тока в линии по аналогии с (9.2) будет определяться выражением
![]() (9.3)
(9.3)
где Im= Um/W — амплитуда тока в линии.
Из формул (9.2) и (9.3) видно, что значения напряжения
и тока гармонической волны в линии определяются как параметрами генератора (![]() , Um), так и параметрами линии
передачи (Vф , W).
Колебательные процессы во всех точках
линии начинаются не одновременно, а с запаздыванием, равным пространственному
набегу фазы волны
, Um), так и параметрами линии
передачи (Vф , W).
Колебательные процессы во всех точках
линии начинаются не одновременно, а с запаздыванием, равным пространственному
набегу фазы волны ![]() x. Бегущая волна
распространяется в линии с конечной скоростью Vф=
x. Бегущая волна
распространяется в линии с конечной скоростью Vф= ![]() /
/![]() .
При этом удаленные от начала линии точки возбуждаются волной позже, чем
близкие. Колебательный процесс во всей линии устанавливается через время t=
1/ Vф .
.
При этом удаленные от начала линии точки возбуждаются волной позже, чем
близкие. Колебательный процесс во всей линии устанавливается через время t=
1/ Vф .
Выражения (9.2) и (9.3) соответствуют бегущей волне,
распространяющейся в идеальной линии от генератора к нагрузке, т.е. падающей
волне (координатная ось Ох направлена от генератора к нагрузке). Бегущая
волна, распространяющаяся н противоположном направлении (отраженная волна),
будет отличаться от падающей только отрицательным знаком фазовой скорости Vф и коэффициента фазы ![]() и, возможно, амплитудой. Поэтому,
считая, что амплитуды отраженной и падающей волн равны, для напряжения
отраженной волны получим следующее выражение:
и, возможно, амплитудой. Поэтому,
считая, что амплитуды отраженной и падающей волн равны, для напряжения
отраженной волны получим следующее выражение:
![]()
![]() (9.4)
(9.4)
9.4. Длинные линии с потерями и без потерь
Линия с потерями. Сопротивление нагрузки Zн оказывает существенные влияния на режим работы длинной линии. Проведем анализ волновых процессов в линии с потерями.
Пусть ![]() и
и ![]() — комплексные амплитуды напряжения и
тока на нагрузке. Расстояние вдоль длинной линии будем отсчитывать от ее конца
(нагрузки) к началу (генератору). При таком выборе системы отсчета комплексные
амплитуды напряжения и тока в линии определяются выражениями:
— комплексные амплитуды напряжения и
тока на нагрузке. Расстояние вдоль длинной линии будем отсчитывать от ее конца
(нагрузки) к началу (генератору). При таком выборе системы отсчета комплексные
амплитуды напряжения и тока в линии определяются выражениями:
![]() (9.5)
(9.5)
![]() (9.6)
(9.6)
где 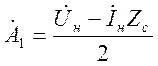 и
и 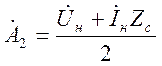 — постоянные коэффициенты, в общем
случае комплексные:
— постоянные коэффициенты, в общем
случае комплексные: ![]() комплексный коэффициент
распространения электромагнитной волны в линии.
комплексный коэффициент
распространения электромагнитной волны в линии.
Комплексный характер волнового сопротивления линии с потерями
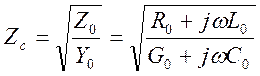
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.