Частотно-избирательные системы. Длинные линии (8-9 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 13

свидетельствует о наличии сдвига фаз между током и напряжением в бегущей волне в линии пере­дачи с потерями. В идеальной линии  и тогда

Комплексный коэффициент распространения электромагнит­ной волны в линии с потерями может быть представлен в виде суммы действительной и мнимой частей

.

Для определения физического смысла этих составляющих ком­плексного коэффициента  запишем выражение для мгновенно­го значения напряжения в линии:

                (9.7)

где U₁и U₂ — амплитудные коэффициенты.

Сравнивая по аналогии правые части выражений (9.2), (9.4) и (9.7), видим, что напряжение, возбуждаемое синусоидальным генератором в линии с потерями, представляет собой сумму двух бегущих волн. При этом первое слагаемое в правой части (9.7) представляет волну напряжения, распространяющуюся от нагруз­ки к генератору (отраженная волна), а второе — волну, бегущую от генератора к нагрузке (падающая волна). Анализируя выраже­ние (9.7), следует помнить, что положительное направление оси Ох в данном случае совпадает с направлением в линии от нагруз­ки к генератору. Амплитуды волн в (9.7) в отличие от волн в (9.2) и (9.4) убывают в направлении распространения каждой из волн за счет экспоненциальных множителей ехр(-х) и ехр(х). Это объясняется тем, что при распространении электромагнит­ной волны в линии с потерями энергия волны уменьшается и соответственно уменьшается амплитуда колебаний в волне. Ко­эффициент а в показателях экспонент в (9.7) называется коэф­фициентом затухания. Он характеризует степень затухания амп­литуды колебаний при распространении волны на единицу дли­ны и имеет размерность 1/м.

На рис. 9.11 показан график распределения напряжения в па­дающей волне вдоль линии в некоторый фиксированный момент времени (координата х' отсчитывается от генератора к нагрузке, а координата х — в противоположном направлении). Из графика видно, что амплитуда напряжения в падающей волне затухает по экспоненциальному закону в направлении от начала к концу ли­нии.

 

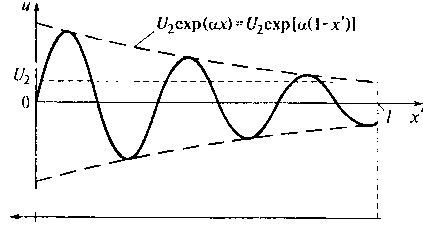Рис. 9.11. Распределение напряжения в падающей волне

Мнимая часть _п комплексного коэффициента  в (9.7) имеет тот же смысл, что и коэффициент фазы волны  в идеальной линии в выражениях (9.2) и (9.3) и поэтому имеет то же название. В общем случае при произвольных потерях в линии коэффициенты фазы _п и  имеют разную зависимость от погонных параметров линии (). В реальных линиях передачи потери доста­точно малы и достоверны соотношения:  и .

При этих условиях выражения для коэффициентов _п и а при­нимают вид:

                                                      

Для двухпроводной линии из медных проводов с радиусом r (мм) на частоте  f(МГц) или длине волны (м) погонное сопро­тивление (Ом/м) с учетом поверхностного эффекта определяется формулой . Таким образом, погонное сопротивление R₀ и, следовательно, коэффициент затухания a являются функциями частоты сигнала и радиуса проводов линии. Чем выше частота колебаний в волне и чем меньше диаметр сече­ния проводов, тем больше потери энергии волны в линии. Поэто­му для снижения потерь в высокочастотных линиях выбирают проводники с большим диаметром сечения проводов.

Линия без потерь. Процессы в линии без потерь мало отличают­ся от процессов в реальных линиях небольшой длины из-за мало­сти потерь в них. Поэтому заменим анализ процессов в реальных линиях анализом идеальной линии.

Для идеальной линии справедливы соотношения: = 0 и . В этом случае амплитуда напряжения в падаю­щей волне вдоль линии остается неизменной. Уравнения для ком­плексных амплитуд напряжения и тока в идеальной линии при­нимают вид:

                                                        (9.8)

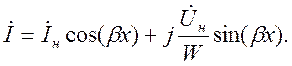                                                           (9-9)

Формулы (9.8) и (9.9) определяют значения полного напря­жения и тока в линии, которые являются суммой соответственно напряжений и токов в падающей и отраженной волнах.

Опираясь на выражения (9.8) и (9.9), можно определить ком­плексное эквивалентное сопротивление линии Z_экв как отноше­ние комплексных амплитуд напряжения и тока в ее произвольном сечении с координатой x:

                                            

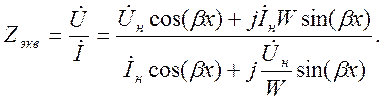
Или после преобразований

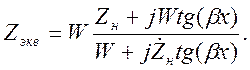                                                                 (9.10)

Эквивалентное сопротивление в общем случае является комп­лексной величиной, измеряется в Ом и зависит от координаты х выбранного сечения длинной линии. При х=lформула (9.10) оп­ределяет эквивалентное сопротивление линии на ее входе, т.е. вход­ное сопротивление линии Z_вх = Z_экв(l). Это равенство выражает очень важный факт: входное сопротивление идеальной линии явля­ется периодической функцией ее длины. Это свойство отрезка линии длиной lиспользуется в диапазоне сверхвысоких частот для пост­роения трансформаторов сопротивлений.

Опираясь на полученные в подразд. 9.4 уравнения длинной ли­нии, рассмотрим ее свойства в различных режимах работы.

9.5. Режим бегущей волны в длинной линии

Режим бегущих волн иначе еще называют режимом с согласованной нагрузкой, так как он существует в линии при ус­ловии Z_н= W. При этом , и уравнения (9.8) и (9.9) с учетом формулы Эйлера  преобразу­ются к виду

                                            

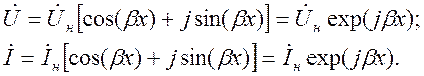
Из этих уравнений находим выражения для мгновенных значе­ний напряжения и тока:

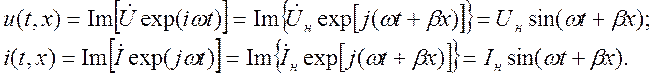
В полученных выражениях принято, что начальные фазы комп­лексных амплитуд напряжения  и тока  равны нулю. Анало­гичные выражения получаются при отсчете координаты х^г = 1-х от начала линии:

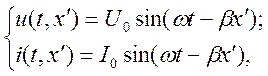                                                             (9.11)

где U₀ и I₀ — амплитуды напряжения и тока в начале линии.