Частотно-избирательные системы. Длинные линии (8-9 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 15

Из анализа полученных выражений вытекают следующие вы­воды:

максимальное значение амплитуды стоячих волн напряжения и тока в 2 раза превышает амплитуды соответствующих падающих и отраженных волн;

при отражении падающей волны напряжения от разомкнутого конца линии фаза ее не меняется, т.е. фазы падающей и отражен­ной волн в конце линии совпадают. Поэтому полное напряжение в любом сечении линии равно сумме напряжений падающей и отраженной волн;

при отражении падающей волны тока от разомкнутого конца линии фаза ее меняется на 180°. Поэтому полный ток в линии равен разности значений токов падающей и отраженной волн. Такое соотношение фаз падающей и отраженной волн тока обусловлено необходимостью равенства нулю полного тока на разомкнутом конце линии.

Рассмотрим свойства стоячих волн в разомкнутой линии. На рис. 9.14 показано распределение напряжения и тока в стоячей волне в идеальной разомкнутой линии в соответствии с формулами (9.14) для равноотстоящих моментов времени t₀, t₁ ...t₈, укладывающихся на одном временном периоде .

На рис. 9.14 видно, что в каждом сечении линии ток и напря­жение изменяются по гармоническому закону в соответствии с множителями cos() и sin(). Причиной этого служит генератор синусоидального напряжения, возбуждающий линию. На рис. 9.14 отмечены последовательными моментами времени t₀, ...t₈ различ­ные фазы колебаний напряжения и тока в линии с учетом сдвига фаз на 90° между cos() и sin(). Однако в отличие от бегущих волн у стоячих волн напряжения и тока амплитуды колебаний U_m и I_m не постоянны вдоль линии, а зависят от координаты х по законам  и  соответственно. Аргументы си­нуса и косинуса здесь являются функциями относительного рас­стояния, отсчитываемого от конца линии в длинах волн: . Как видно на рис. 9.14, на расстояниях от конца линии, кратных половине длины волны, т.е. при  или , где п = 0, 1, 2, ..., амплитуда напряжения максимальна , а амплитуда тока равна нулю. Соответствующие сечения линии называются пуч­ностями напряжения и узлами тока. С другой стороны, на расстояниях от конца линии, кратных нечетному числу  /4, т.е. при  или , где p = 1, 3, 5, ..., амплитуда напряже­ния равна нулю, а амплитуда тока достигает максимума . Такие сечения линии называются узлами напряжения и пучностя­ми тока.

 

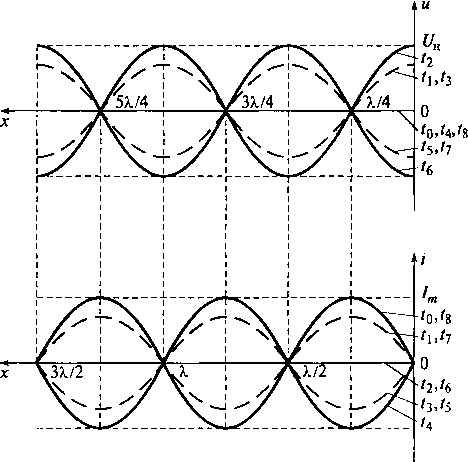Рис. 9.14. Распределение напряжения и тока в стоячей волне в идеальной

разомкнутой линии

Из уравнений (9.14) видно, что фаза напряжения t в стоячей волне не зависит от координаты х сечения длинной линии. Это означает, что колебания напряжения во всех сечениях линии про­исходят синфазно, т.е. напряжение вдоль всей линии одновре­менно достигает максимума, нулевого значения, минимума и всех промежуточных значений. Однако амплитуда колебаний напряже­ния в различных сечениях линии разная.

То же самое можно сказать и о синфазности колебаний тока в линии в соответствии с уравнением стоячей волны тока (9.14). При сравнении законов колебания напряжения и тока в линии видно, что между ними в отличие от бегущих волн существует сдвиг фаз во времени, равный 90°.

Так как колебания напряжения (или тока) в стоячей волне в линии происходят синфазно, то положения узлов и пучностей напряжения (и тока) остаются неизменными, т.е. они как бы стоят. Отсюда и происходит название «стоячая» волна.

Из системы уравнений (9.14) следует, что отношение ампли­туд напряжения и тока в пучностях равно волновому сопротивле­нию линии W. Этот факт может быть использован для определе­ния неизвестного волнового сопротивления линии.

Из графиков пространственно-временной картины колебаний в стоячей волне на рис. 9.14 можно сделать еще один интересный вывод: пространственный период колебаний в стоячей волне ра­вен /2, т.е. в 2 раза меньше, чем в бегущей волне.

Рассмотренные свойства стоячих волн показывают, что эти волны существенно отличаются от бегущих, в которых мгновен­ные значения напряжения и тока изменяются по длине идеаль­ной линии из-за изменения фазы, а в стоячих волнах — из-за изменения амплитуды. В стоячих волнах фазы напряжения и тока сдвинуты на 90°, а в бегущих волнах они совпадают. Кроме того, в бегущих волнах пространственный сдвиг между напряжением и током отсутствует, а в стоячих волнах он равен л/4 из-за чего в них пучности напряжения совпадают с узлами тока, а узлы на­пряжения совмещены с пучностями тока.

В соответствии с уравнением (9.10) эквивалентное сопротив­ление разомкнутой идеальной линии при  определяется выражением

                                                                                                               (9-15)

Реактивный характер эквивалентного сопротивления обуслов­лен тем, что в стоячей волне между током и напряжением суще­ствует фазовый сдвиг 90°. В связи с этим и средняя мощность, отдаваемая генератором в разомкнутую линию без потерь, равна нулю.

Распределение эквивалентного сопротивления вдоль идеальной разомкнутой длинной линии от координаты сечения х показан на рис. 9.15. Оно имеет периодический характер с периодом /2, т.е. равным периоду стоячей волны. На участках линии, удовлетворя­ющих условию  эквивалент­ное сопротивление линии Z_экв.хх изменяется от -j8 до j8. В сече­ниях х = (п + 1) /4 (n = 0, 1,2, ...) эквивалентное сопротивление Z_экв.хх обращается в нуль, что объясняется совпадением этих сече­ний с узлами напряжения в стоячей волне. В сечениях разомкнутой идеальной линии с координатами х = п/2, (п = О, 1, 2, ...), соот­ветствующим пучностям напряжения и узлам тока, Z_экв.хх.

 

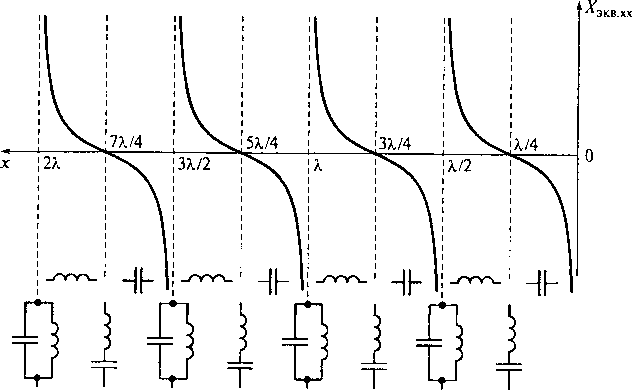Рис. 9.15. Распределение эквивалентного сопротивления вдоль идеальной разомкнутой длинной линии