Частотно-избирательные системы. Длинные линии (8-9 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 14

Сравнение выражений (9.11) с (9.2) и (9.3) показывает, что в режиме с согласованной нагрузкой в линии существуют только падающие волны напряжения и тока. Отраженных волн в линии нет. Следовательно, энергия, которую несет падающая электро­магнитная волна, полностью поглощается в нагрузке.

Напряжение и ток в линии в режиме бегущей волны, как вид­но из (9.11), в каждом сечении х' изменяются во времени по си­нусоидальному закону. Это связано с синусоидальным законом изменения напряжения  на выходе генератора (вхо­де линии).

По мере распространения волны вдоль линии координата х' увеличивается, а фаза бегущей волны  уменьшается. Это означает, что в сечениях x, более удаленных от начала линии, синусоидальные колебания во времени воспроизводятся с боль­шим отставанием по фазе по сравнению с колебаниями в начале линии. Это отставание по фазе обусловлено конечной фазовой скоростью V_фволны в линии. На рис. 9.12 показаны временные диаграммы колебаний в волне для различных сечений длинной линии.

Отсутствие потерь энергии в идеальной линии обусловливает независимость амплитуды колебаний напряжения и тока в бегу­щей волне от координаты сечений линии (см. рис. 9.12).

Вдоль линии для фиксированного момента времени напряжение, и ток тоже изменяются по синусоидальному закону. С течени­ем времени картина этого распределения перемешается от гене­ратора к нагрузке.

Входное сопротивление идеальной линии в режиме бегущих волн при условии Z_н=W и  можно найти по формуле (9.10): Z_вх = Z_экв(l) = W. Следовательно, в режиме бегущих волн входное сопротивление линии является действительным и равным ее вол­новому сопротивлению. Кроме того, из формулы (9.10) следует, что при условии согласования (Z_н=W) для любого x выполняет­ся равенство Z_экв=W. Это еще раз подтверждает сделанный ранее вывод о том, что волновое сопротивление линии W — это сопро­тивление, которое оказывает линия бегущей волне. Оно активно и постоянно на всем протяжении линии, в том числе и на ее входе (выходе генератора). Для бегущей волны в идеальной линии колебания напряжения и тока в волне всюду совпадают по фазе, т.е. они одновременно достигают максимума и минимума.

 

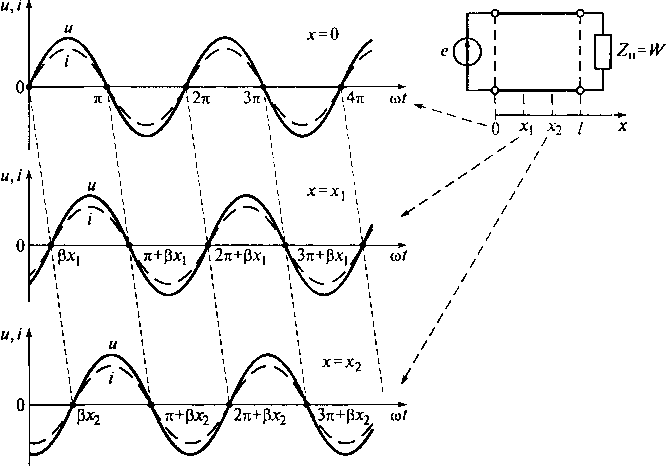Рис. 9.12, Временные диаграммы колебаний в бегущей волне для различ­ных сечений длинной линии

Режим бегущих волн нарушается в местах, где линия имеет неоднородности, или при несогласованности ее с нагрузкой. Вслед­ствие этого волновым сопротивлением линии называют также входное сопротивление бесконечно длинной однородной линии.

На практике в большинстве случаев условие согласования ли­нии и нагрузки Z_н=W не выполняется, поэтому для обеспечения режима бегущих волн в линии используются различные согласую­щие устройства. Простейшее из них — четвертьволновый транс­форматор, представляющий собой отрезок линии длиной /4 с волновым сопротивлением W_тр. В этом согласующем устройстве используется свойство отрезка линии трансформировать сопро­тивление нагрузки. При длине линии l=/4 пространственный набег фазы волны

                                                

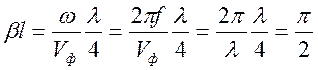
При таком набеге фазы в соответствии с (9.10) входное сопро­тивление четвертьволнового отрезка линии

                                                                               (9.12)

 

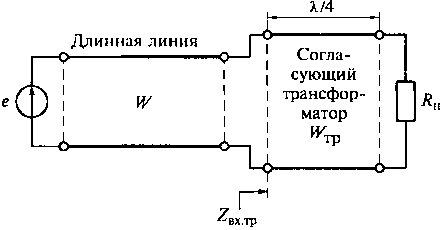Рис. 9.13. Согласование линии с активной нагрузкой с помощью чет­вертьволнового трансформатора

Для согласования активного сопротивления нагрузки (Z_н = R_н) трансформатор включается между концом линии и нагрузкой. Ус­ловие согласования выполняется при W = Z_вх.тp. На рис. 9.13 пока­зано согласование линии с активной нагрузкой с помощью чет­вертьволнового трансформатора.

При заданных значениях активных сопротивлений Wи R_Hиз (9.12) получим выражение для необходимого волнового сопро­тивления трансформатора

                                                                                   (9.13)

Подбор волнового сопротивления трансформатора W_трв соот­ветствии с условием (9.13) позволяет согласовать линию с на­грузкой на рабочей длине волны . Четвертьволновый трансфор­матор является узкополосным согласующим устройством, так как при изменении рабочей длины волны нарушается условие l=/4 и соответственно не выполняются условия (9.12) и (9.13) согла­сования линии с нагрузкой.

9.6. Режим стоячих волн в длинной линии

Стоячая волна возникает в линии передачи в результате сложе­ния равных по амплитуде падающей и отраженной волн, что воз­можно только в идеальной линии, нагрузка которой не поглоща­ет энергии.

Существует три типа нагрузок, которые обладают этим свой­ством, а именно:

бесконечно большая нагрузка — линия разомкнута на конце (режим холостого хода);

значение величины нагрузки равно нулю — линия замкнута на конце (режим короткого замыкания);

реактивная нагрузка.

Режим холостого хода. При холостом ходе линии I_н= 0 и урав­нения (9.9) для комплексных амплитуд напряжения и тока при­нимают вид

                       

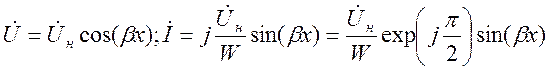
Положим, что фаза комплексной амплитуды напряжения на конце линии (x = 0) равна нулю, т.е., и перейдем к мгно­венным значениям напряжения и тока:

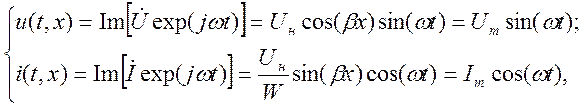       (9.14)

где — амплитуды колебаний на­пряжения и тока.

Полученные выражения представляют собой уравнения для стоячих волн напряжения и тока в линии при режиме холостого хода. В этом можно убедиться, воспользовавшись тригонометри­ческими тождествами:

                       

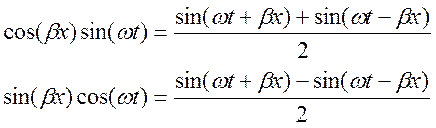
С учетом этих тождеств уравнения (9.14) принимают следую­щий вид:

                         

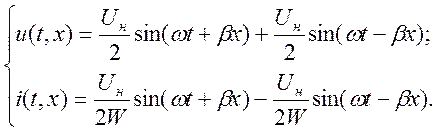
Каждое из слагаемых в правых частях полученных уравнений представляет собой бегущую волну. При этом первые слагаемые — это падающие волны, распространяющиеся от генератора к кон­цу линии, а вторые слагаемые — это отраженные волны, бегущие от разомкнутого конца линии к ее началу.