Частотно-избирательные системы. Длинные линии (8-9 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 16

Входное сопротивление идеальной разомкнутой линии также определяется формулой (9.15) при подстановке в нее х = l. При  мнимая часть Х_экялк отрицательна, и входное сопротивле­ние линии носит емкостный характер. При /4 < I < /2 из рис. 9.15 видно, что X_эквхх> 0 и входное сопротивление линии носит индук­тивный характер. Такое поведение входного сопротивления будет повторяться при увеличении длины линии / на целое число полу­волн.

Входное сопротивление разомкнутой линии с потерями имеет активную составляющую R_эквхх Реактивная составляющая X_вxхх несколько изменяет характер своего поведения по сравнению с величиной X_эквхх. На рис. 9.16 показана зависимость составляющих входного сопротивления разомкнутой длинной линии с потерями от ее длины. Реактивная составляющая входного сопротивления разомкнутой линии периодически изменяется в конечных сим­метричных пределах около нуля при изменении длины линии (или длины волны) и обращается в нуль при условии 1 = п/4, (п = 0,1, 2,...). Сечения линии, в которых реактивная составляющая вход­ного сопротивления обращается в нуль, называются резонансными. Активная составляющая входного сопротивления R_эквхх изменяет­ся с периодом /2, оставаясь положительной величиной, дости­гающей максимального значения при тех длинах линии, при ко­торых на входе линии существует пучность напряжения и мини­мум тока, т.е. при l= п/2, где п = О, 1, 2, ....

Активная составляющая R_эквхх при l = (2n + 1) /4, где п = 0,1,2,  ... имеет минимальное значение, так как при этом условии на входе линии имеется минимум напряжения и пучность тока.

 

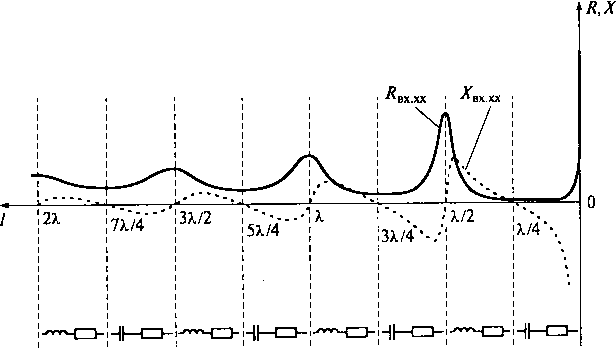Рис. 9.16. Зависимость составляющих входного сопротивления разомкну­той длинной линии с потерями от ее длины

Режим короткого замыкания. В короткозамкнутой линии сопро­тивление нагрузки Z_H равна нулю. Амплитуда напряжения на на­грузке U_hв этом случае также равна нулю, и уравнения (9.8) и (9.9) для комплексных амплитуд напряжения и тока в идеальной линии принимают вид:  и .

Положим, что начальная фаза тока в конце линии равна нулю, т.е. . Перейдем при этом условии от комплексных амплитуд к мгновенным значениям напряжения и тока в линии;

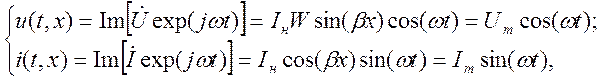
где  — зависящие от координаты сечения линии х амплитуды напряжения и тока.

Полученные уравнения для полного напряжения и тока в ли­нии являются уравнениями стоячих волн. Сравнение их с уравне­ниями (9.14) показывает, что в случае короткого замыкания кар­тины распределения амплитуд тока и напряжения вдоль линии поменялись местами в сравнении со случаем холостого хода. Гра­фики распределения амплитуд напряжения и тока вдоль линии при коротком замыкании получаются сдвигом соответствующих графиков для режима холостого хода к концу линии на расстоя­ние /4. Как и в случае холостого хода линии, правые части выра­жений (9.14) можно представить в виде линейных комбинаций падающей и отраженной волн с равными, но вдвое меньшими амплитудами. При этом полное напряжение равно разности на­пряжений падающей и отраженной волн. Это означает, что при отражении от короткозамкнутого конца линии фаза отраженной волны напряжения изменяется на 180° по сравнению с падающей волной. Только в этом случае полное напряжение на конце линии будет равно нулю. Полный ток в линии при коротком замыкании равен сумме токов падающей и отраженной волн. Фаза тока при отражении от короткозамкнутого конца линии не меняется, а амплитуда полного тока на конце линии имеет пучность и удваи­вается по сравнению с ее значением в падающей волне.

Указанные особенности стоячей волны для режима короткого замыкания линии показаны на рис. 9.17, на котором приведены графики распределения амплитуд напряжения и тока в идеальной короткозамкнутой линии.

В короткозамкнутой линии с потерями вследствие наличия до­полнительной бегущей волны узлы (нули) в распределении тока и напряжения становятся минимумами, не равными нулю, а ам­плитуды в пучностях становятся меньше удвоенного значения амплитуды бегущей волны.

 

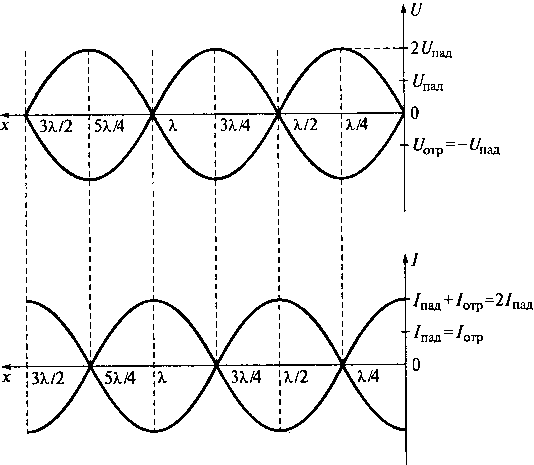Рис. 9.17. Графики распределения амплитуд напряжения и тока в идеаль­ной короткозамкнутой линии

При Z_H= 0 из (9.10) находим выражение для эквивалентного сопротивления короткозамкнутой линии: Z_экв.кз, где  — мнимая часть эквивалентного сопротивления.

Реактивный характер эквивалентного сопротивления связан со сдвигом по фазе на 90° колебаний напряжения и тока в стоячей волне во времени.

Входное сопротивление идеальной короткозамкнутой линии получается при . Зависимость входного сопротивления от длины короткозамкну­той линии без потерь и с потерями показана на рис. 9.18.

Входное сопротивление идеальной короткозамкнутой линии равно нулю при l = n/2, _где п = 0, 1, 2, ..., т.е. когда на входе линии имеется узел напряжения. Если на входе линии имеется узел тока, т.е. l = (2п + 1) /4, где п = О, 1, 2, ..., то ее входное сопротивление стремится к бесконечности. При 0 < l < /4 вход­ное сопротивление короткозамкнутой линии без потерь положи­тельно, т.е. имеет индуктивный характер, а при /4 < l < /2 оно отрицательно и является емкостным. Значения входного сопро­тивления линии повторяются при увеличении ее длины на n/2, где п = 1, 2, 3 ... .

В реальной короткозамкнутой линии с потерями кроме основ­ной стоячей волны имеется еще некоторая бегущая волна, рас­пространяющаяся от генератора к концу линии и компенсирующая потери энергии в ней. Наличие дополнительной бегущей вол­ны обусловливает появление активной составляющей во входном сопротивлении линии. Зависимость активной R_вхжз и реактивной X_вхжз составляющих входного сопротивления короткозамкнутой линии с потерями показана на рис. 9.18, б. Приведенные графики, как и все предыдущие для режима короткого замыкания линии, получены сдвигом на /4 к концу линии соответствующих графи-

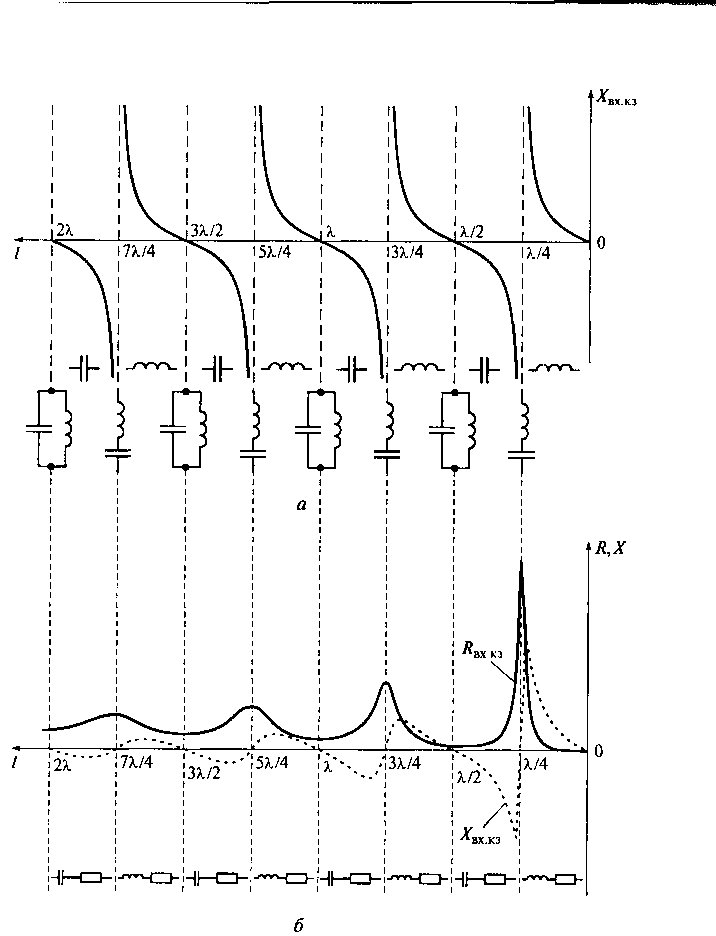
Рис. 9.18. Зависимость входного сопротивления от длины короткозамкну­той линии без потерь (а) и с потерями (б)