На рис. 9.7 показаны эквивалентные схемы замещения
бесконечной идеальной длинной линии и графики распределения напряжения и тока
вдоль нее в моменты t = ![]() tи t
= 2
tи t
= 2![]() t. В этих схемах
t. В этих схемах ![]() . Схемы на рис. 9.7, а, в упростят рассмотрение
электромагнитных процессов в бесконечно длинной волне. На эквивалентной схеме
на рис. 9.7, а отображено только первое элементарное звено, нагруженное
на активное волновое сопротивление линии W, имитирующее оставшуюся бесконечную часть схемы
замещения.
. Схемы на рис. 9.7, а, в упростят рассмотрение
электромагнитных процессов в бесконечно длинной волне. На эквивалентной схеме
на рис. 9.7, а отображено только первое элементарное звено, нагруженное
на активное волновое сопротивление линии W, имитирующее оставшуюся бесконечную часть схемы
замещения.
Пусть в момент t
= 0 замыканием ключа S(см. рис.
9.7, а) к линии подключается источник постоянного напряжения E0. В этом случае через
индуктивность ![]() L1 потечет ток i0 = E0/W.
Так как сопротивление W активно, то ток
i0
совпадает по фазе с напряжением E0. Этот ток в точке разветвления схемы разбивается на две
составляющие, первая из которых icзаряжает емкость
L1 потечет ток i0 = E0/W.
Так как сопротивление W активно, то ток
i0
совпадает по фазе с напряжением E0. Этот ток в точке разветвления схемы разбивается на две
составляющие, первая из которых icзаряжает емкость ![]() С1
а вторая iw
протекает через активное эквивалентное нагрузочное сопротивление W,причем i0 = iс + iw.
С1
а вторая iw
протекает через активное эквивалентное нагрузочное сопротивление W,причем i0 = iс + iw.
В начальный момент при t = 0 ток iс практически равен току i0, а ток iw
близок к нулю. По мере заряда емкости
конденсатора ![]() С1 ток iс уменьшается, а напряжение
на конденсаторе возрастает; ток iw в
это же время также растет.
С1 ток iс уменьшается, а напряжение
на конденсаторе возрастает; ток iw в
это же время также растет.
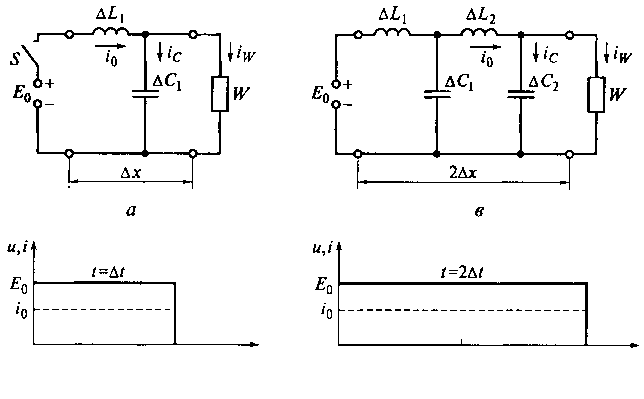 |
Рис. 9.7. Эквивалентные схемы замещения бесконечной идеальной длинной линии (а, в) и графики распределения напряжения и тока (б, г)
Через некоторое время ![]() tпосле
подключения источника напряжения к линии заряд емкости конденсатора первого
звена практически завершается, напряжение на нем достигает значения близкого к E0, ток iс падает почти до нуля. При
этом ток iw становится
приблизительно равным i0. Таким
образом, к концу интервала времени
tпосле
подключения источника напряжения к линии заряд емкости конденсатора первого
звена практически завершается, напряжение на нем достигает значения близкого к E0, ток iс падает почти до нуля. При
этом ток iw становится
приблизительно равным i0. Таким
образом, к концу интервала времени ![]() tна
начальном участке линии длиной
tна
начальном участке линии длиной ![]() х, соответствующем
первому низкочастотному звену схемы замещения, напряжение и ток достигнут
установившихся постоянных значений E0 и i0 (см.
рис. 9.7, б).
х, соответствующем
первому низкочастотному звену схемы замещения, напряжение и ток достигнут
установившихся постоянных значений E0 и i0 (см.
рис. 9.7, б).
На следующем интервале времени ![]() весь
описанный процесс повторится на втором элементарном участке эквивалентной
схемы (см. рис. 9.7, в). К моменту времени t= 2
весь
описанный процесс повторится на втором элементарном участке эквивалентной
схемы (см. рис. 9.7, в). К моменту времени t= 2![]() tна этом
участке ток и напряжение также достигнут своих постоянных значений i0 и E0(см. рис. 9.7, г).
tна этом
участке ток и напряжение также достигнут своих постоянных значений i0 и E0(см. рис. 9.7, г).
Таким образом, процесс заряда элементарных емкостей ![]() С через элементарные
индуктивности
С через элементарные
индуктивности ![]() Lсоздает волны тока и напряжения (в
рассматриваемом приближении с прямоугольными фронтами), распространяющиеся от
источника вдоль линии. Такие волны называются бегущими. Бегущие волны,
распространяющиеся вдоль линии от источника, называются падающими, а к источнику
— отраженными. Как видно на рис. 9.7, на всех элементарных участках линии,
охваченных падающими волнами, устанавливаются постоянные напряжение и ток.
Lсоздает волны тока и напряжения (в
рассматриваемом приближении с прямоугольными фронтами), распространяющиеся от
источника вдоль линии. Такие волны называются бегущими. Бегущие волны,
распространяющиеся вдоль линии от источника, называются падающими, а к источнику
— отраженными. Как видно на рис. 9.7, на всех элементарных участках линии,
охваченных падающими волнами, устанавливаются постоянные напряжение и ток.
Внесем два уточнения в характер протекания процессов в линии, связанных с приближенным представлением линии схемой замещения. На рис. 9.7, б, г фронт волны показан в форме прямоугольной ступеньки и разделяет всю линию на два участка — правый и левый. На левом участке, полностью охваченном волной, ток и напряжение имеют установившиеся значения i0 и E0, а на правом участке, куда волна еще не пришла, их значения равны нулю.
Первое уточнение связано с характером движения фронта
волны. Как было показано, фронт волны перемещается вдоль линии скачками на
расстояние ![]() х по истечении очередного интервала времени
х по истечении очередного интервала времени ![]() t. Реально
же фронт волны перемещается плавно, без скачков. Кажущееся скачкообразное
движение фронта волны возникает из-за того, что идеальная линия с непрерывно
распределенными параметрами была заменена схемой замещения с сосредоточенными
параметрами
t. Реально
же фронт волны перемещается плавно, без скачков. Кажущееся скачкообразное
движение фронта волны возникает из-за того, что идеальная линия с непрерывно
распределенными параметрами была заменена схемой замещения с сосредоточенными
параметрами ![]() Lи
Lи ![]() С
конечной величины. Если в схеме замещения элементарные участки с конечной
длиной
С
конечной величины. Если в схеме замещения элементарные участки с конечной
длиной ![]() х заменить участками с бесконечно
малой длиной dx и с соответственно бесконечно малыми параметрами dL = L()dxи dC = C0dx, то время заряда емкостей dC будет тоже
бесконечно малым и равным d/. При этом фронт волны будет перемещаться непрерывно
со скоростью V= dx/dt, равной фазовой скорости
волны Vф.
х заменить участками с бесконечно
малой длиной dx и с соответственно бесконечно малыми параметрами dL = L()dxи dC = C0dx, то время заряда емкостей dC будет тоже
бесконечно малым и равным d/. При этом фронт волны будет перемещаться непрерывно
со скоростью V= dx/dt, равной фазовой скорости
волны Vф.
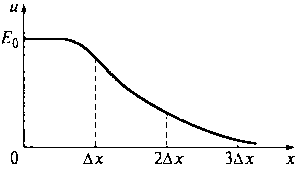 |
Рис. 9.8. Искажение фронта волны в бесконечной идеальной длинной линии
Второе уточнение связано с формой фронта волны.
Обратимся вновь к рис. 9.7, а, в. Фронты волн тока или напряжения будут иметь
форму ступеньки, если ток iw
будет изменяться мгновенно в конце интервала времени ![]() t от нуля до
значения i0. Однако
этого не происходит, поскольку ток iw меняется в течение интервала времени
t от нуля до
значения i0. Однако
этого не происходит, поскольку ток iw меняется в течение интервала времени ![]() t
непрерывно по нелинейному закону. В
результате одновременно с емкостью
t
непрерывно по нелинейному закону. В
результате одновременно с емкостью ![]() С1
будет заряжаться и емкость
С1
будет заряжаться и емкость ![]() С2
следующего звена схемы замещения, только током с меньшим значением. Когда к
концу первого интервала времени
С2
следующего звена схемы замещения, только током с меньшим значением. Когда к
концу первого интервала времени ![]() t
на емкости
t
на емкости ![]() С1
установится напряжение E0, на
емкости
С1
установится напряжение E0, на
емкости ![]() С2 тоже будет
существовать некоторое меньшее напряжение. По той же причине на емкостях
последующих элементарных участков установятся напряжения, значения которых
будут убывать по нелинейному закону с ростом номера элементарной ячейки. Таким
образом, фронт волны будет криволинейным. На рис. 9.8 показано искажение фронта
волны в бесконечной идеальной длинной линии.
С2 тоже будет
существовать некоторое меньшее напряжение. По той же причине на емкостях
последующих элементарных участков установятся напряжения, значения которых
будут убывать по нелинейному закону с ростом номера элементарной ячейки. Таким
образом, фронт волны будет криволинейным. На рис. 9.8 показано искажение фронта
волны в бесконечной идеальной длинной линии.
Искажение фронта волны (его длительность) будет тем больше, чем большими значениями погонных параметров L0 и С0 характеризуется линия.
При распространении волны напряжения вдоль длинной линии на поверхности ее проводов появляется заряд q, погонное значение которого q0= C0E0. Перемещаясь вдоль линии на расстояние dxзавремя dt, волна напряжения сообщает линии дополнительный заряд dq = q0dx=C0E0dx. Можно сказать, что этот заряд распространяется вдоль линии от источника до точки расположения фронта волны напряжения или тока. Это эквивалентно тому, что в линии наряду с волнами тока и напряжения существует волна заряда. Ток и заряд в волне связаны соотношением
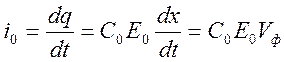
Учитывая, что ![]() ,
получим выражение для фазовой скорости волны в идеальной длинной линии
,
получим выражение для фазовой скорости волны в идеальной длинной линии
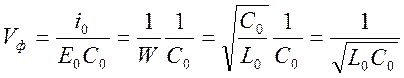
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.