Тепломассообмен (физико-математические основы): Учебное пособие, страница 49

М – общее  число  элементов  сетки; Ф_n- элементный  вклад,  определя-  емый  равенством

.

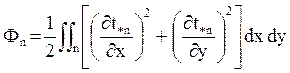Для  произвольного  элемента  n  в  форме  треугольника  функция  формы  выбирается  линейной,  то  есть  t_*n(x,y) = a_n + b_nx + c_ny,  x,y.  Постоян-ные  a_n, b_n, c_n  в  общем  случае  различны  для  разных  элементов.

Для  их  определения  запишем  функции  формы  для  узлов  i, k, j:

t_i = a + bx_i + cy_i,  t_k = a + bx_k + cy_k,  t_j = a + bx_j + cy_j .  Здесь  t_i, t_k, t_j – значения  температуры  в  узлах  i, k, j  соответственно;  индекс  n  опущен  для  упрощения  записи.

Решая  эту  систему  уравнений,  выразим  коэффициенты  через  t:

    .

Здесь  - площадь  треугольника  (n)  равная 

Эту  формулу  можно  получить,  если  из  площади  прямоугольника,  рав-ной  произведению (x_j  x_i) (y_k – y_i),  исключить  площади  трех  треугольни-ков,  расположенных  в  углах  прямоугольника  x_iy_k, y_kx_j, y_ix_j .

Коэффициенты  κ, χ, ν  также  выражаются  через  координаты  узлов.

Например,  κ_i = x_jy_k – x_ky_j;  χ_i = y_k – y_i;  ν_i = x_j – x_k.

Теперь  . Дифференцируя  это  выражение,  получим

и  элементный  вклад  n-ого  треугольника

Выражение  в  квадратных  скобках  не  зависит  от  x  и  y,  а  интег-рал  ,  очевидно,  даст  .  Тогда

Такие  выражения  можно  получить  для  всех  М  элементов  и  под-ставить  их  в  функционал  Ф = . Теперь  он  будет  функцией  всех  узловых  значений  t₁, t₂,…t_N .  Узловые  параметры  t_z – это  переменные,  которые  нужно  определить.

Условия  минимума  функционала  Ф  могут  быть  записаны  как     Здесь  при  суммировании  следует  иметь  в  виду,  что  эле-менты,  не  содержащие  узел  z,  имеют  нулевой  вклад.

Уравнения,  вытекающие  из  условия  минимума  функционала,  бу-дут  алгебраическими  уравнениями разностной  схемы  метода  конечных  элементов  относительно  искомых  температур  в  узлах.

В  методе  граничных  элементов  для  аппроксимации искомых  функций  также  используются  интегральные  уравнения,  но  не  в  области  Д,  а  на  ее границе Г.  Это  дает  возможность  вместо  трехмерной  решать  двухмерную  задачу, а вместо двухмерной – одномер-ную,  на  ограничивающем  плоскую  область  контуре.

В  теоретической  основе  метода  лежит  переход  от  задачи,  описы-ваемой  дифференциальными  уравнениями  с  частными  производными,  к  ее  интегральной  формулировке.  Но  эта  формулировка  включает  интегралы  от  искомых  функций  и  их  производных,  вычисляемых  лишь  по  границе  области.  К  таким  интегралам  искомых  функций  относится,  например,  фундаментальное  уравнение  стационарной  тепло-  проводности  для  двухмерного  поля  t(x,x₀) = - ln [|x–x₀|/R₀]  ( где R₀- неко-торое  произвольно  выбранное  расстояние,  вроде  характерного  размера  рассматриваемой  области),  а  также  знакомое  нам уравнение  нестаци-  онарной  теплопроводности 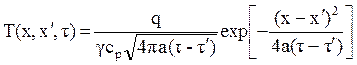 .  Оба  уравнения  описывают  изменение  температурного  поля  в  точке  х,  выз-ванное  мгновенным  выделением  тепла.

Первым этапом  численного  решения  граничных  интегральных  уравнений  является  аппроксимация  искомых  функций и  функций,  заданных  в  граничных  условиях,  на  границе  области  Д.  Для  этой  цели  граница  разбивается  на  элементы  в  виде  отрезков (одномерное  поле),  трех-  или  четырехугольников.  Криволинейные  участки  можно  принимать  плоскими.  Это  упрощает  решение.  В  простейшем  варианте  метода  в  каждом  граничном  элементе  можно  взять  один  узел,  помес-тив  его  в  средину  элемента.  Это  значит,  что  в  пределах  каждого  эле-мента  функции  будут  аппроксимироваться  их  узловыми  значениями.

Аппроксимация  гранично-элементных  функций  многочленами  в  пределах  граничных  элементов  и  вычисление  получающихся  при  этом интегралов  аналогичны  соответствующим  процедурам,  используемым  в  методе  конечных  элементов.