Тепломассообмен (физико-математические основы): Учебное пособие, страница 31

Метод  анализа  размерностей  используют  в  очень   сложных  случаях,  когда  для  процесса  невозможно  составить  систему  дифференциальных  уравнений  вследствие  его  сравнительно  малой изученности. Но  полный  перечень  физических  величин,  существенных  для  данного  процесса,  то  есть  тех,  которые  вошли  бы  в  дифференциальные  уравнения  и  в  условия  однозначности,  должен  быть  известен. Из  них  и  составляют  безразмерные  комплексы.  При  этом  учитывают  требования  p-теоремы,  согласно  которой  число  безразмерных  переменных  p  при  общем  числе  размерных  переменных  n  и  числе  первичных (время,  длина,  масса,  температура,  сила  тока)  переменных  k  равно  n – k.  В  тех  случаях,  когда  перечень  величин,  существенных  для  данного  процесса,  и  их  связь  с  первичными  величинами  установлены  точно,  метод  анализа  размерностей  обеспечивает  результаты,  эквивалентные  методу  масштабных преобразо- ваний. 

Несложные  уравнения  легко  перевести  в безразмерную   форму, ком- бинируя  входящие  в  них  величины.  Рассмотрим эту  возможность  на  примере  конвективного  теплообмена  в  вертикальной  трубе  при  движении  среды  сверху  вниз,  в  направлении  оси  х.  Поля  скорости  w_x  и темпера- туры    t  примем   одномерными,  неустановившимися  во  времени.  Тогда  в  цилиндрической  системе  координат  будем  иметь

·  уравнение  неразрывности  (¶w_x/¶x) = 0;

·  уравнение  теплообмена    a ( t _п -  t) =  - l (¶t/¶ r)_п;

·  уравнение  переноса  энергии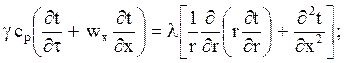

·  уравнение  движения 

·  физические  условия  однозначности: с_р = const ; l = const;m = const;   g = const;

·  начальные  условия:  w(0,) = w₀= const; t(0,) = t ₀ = const;  p(0,) =    = p₀ = const;

·  граничные  условия:  w_{x (y = R)} = 0;  t _{y = R} = t_п = const.

В  качестве   масштабов  выберем  диаметр  канала  d,  скорость  w₀  и  температуру  t _п(поверхности  стенки канала).

Выразим  скорость   w_x  и  координату  х  через  масштабы  w₀ ,  d  и  безразмерные  переменные  V  и   X:  w_x = w₀·V,   x = d·X.  Подставим  их  в  уравнение  неразрывности:  (w₀ ¶V/d ¶X) = 0,  или   (¶V/¶X) = 0.

Никаких   безразмерных  комплексов  данное  уравнение  не  даёт, оно  только  позволяет  упростить  уравнения  движения  и  теплопереноса.

Выразим  температуру  t   и   радиус  r  через  масштабы  t _п , d  и без - размерные  переменные  Q  и  L:  t = t_п·Q,  r = d·L.  Подставив  их  в  уравнение  теплообмена,  после  сокращения  t_п  и  умножения  на   d/l,  получим                          (a d/) (1- Q) = - ¶Q/¶L.

Комплекс  (ad / l) = Nu  есть   критерий  Нуссельта,  в  который  входит  обычно неизвестный коэффициент теплоотдачи a. На  основании  последнего  варианта  уравнения  теплоотдачи   можно  написать: Nu = f (Q,L).

Воспользовавшись  теми  же  выражениями  для  t,  w_x,  r  и  х, уравне- ние    теплопереноса  преобразуем  к  виду

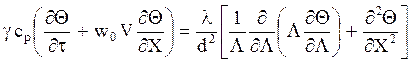
Умножив  обе  части  уравнения  на  d ²/l ,  раскрыв  скобки  в  левой  части  и  введя  d²g c_p/l  под  знак  дифференциала  в  знаменателе  первого  слагаемого,  получим  его  в  виде  ¶Q/¶(lt/d ²gc_p). Отношение  l/gc_p = a   называют  коэффициентом  температуропроводности,  а  комплекс        (аt/d²) = Fo  называют  критерием Фурье. Перед  вторым  слагаемым  левой  части  получается  комплекс (w₀d/a) = Pe,  называемый  критерием  Пекле.

Таким  образом,  окончательно  уравнение  теплопереноса  примет  вид

Отсюда  видно,  что  безразмерная  температура  Q = ( Fo, Pe, V, X, L)  и  что  тогда  Nu = f₁( Fo, Pe, V, X, L).

Используя  те  же  выражения  размерных  переменных  через  безразмерные,  преобразуем  уравнение  движения: