Мы рассмотрели некоторые вопросы, связанные с построением конечно-разностных схем путем разложения функций в ряд Тейлора. Такой способ получения дискретных аналогов прост, но, во-первых, не способствует пониманию физического смысла членов уравнения, а, во-вторых, иногда приводит к схемам, имеющим большую погрешность из-за нарушения законов сохранения энергии, массы, количества движения. Это нарушение обусловлено появлением членов, величина вклада которых в общий баланс определяется не физическими законами, а дискретизацией задачи.
Разностные схемы, при которых получаются численные решения, удовлетворяющие законам сохранения, называются консервативными.
Для построения консервативных схем используется интегроинтерпо-ляционный метод – метод элементарных балансов. При этом область, в которой ищется решение, разбивается на элементарные объемы(ячейки), построенные вокруг каждого узла сетки; границы объемов выбираются в срединах отрезков, образованных соседними узлами сетки, причем сами отрезки не обязательно должны быть равными. Но равенство отрезков в некоторых случаях упрощает расчетные уравнения.
Вычислительная практика показала, что конечно-разностные схемы целесообразно, как правило, применять для элементарных объемов, огра-ниченных поверхностями, параллельными координатным поверхностям. Для декартовых координат это прямоугольники и параллелепипеды, для цилиндрических – кольцевой сектор толщиной dr, с углом раскрытия dφ, длиной dz. Сетка должна быть непосредственно связана с характером изменения зависимой переменной в расчетной области – мелкая сетка необходима там, где эта зависимость от координат является крутой. Ха-рактер изменения переменной может быть принят на основе общих фи-зических представлений о процессе или на основе предварительных ре-шений на сетке с крупным шагом.
Для всех внутренних и граничных точек записывают балансовые уравнения в дифференциальной форме и интегрируют их по каждому контрольному объему. Для вычисления интегралов используют кусочные профили, описывающие изменение переменных между узловыми точками. Часто для этого используют кусочно-линейный профиль, у которого изменение переменной между узловыми точками описывается линейными интерполяционными уравнениями.
В результате интегрирования получают конечно-разностный аналог дифференциального уравнения, в который входят значения переменной в узловых точках.
В качестве примера рассмотрим процесс теплопроводности в цилиндре с изменением температуры по радиусу и по окружности. Выде-лим объем ΔV в виде призмы длиной Δz с поперечным сечением в фор-ме кольцевого сектора 1,2,3,4 (рисунок 18), имеющего размеры Δr, r3Δφ, r4Δφ.
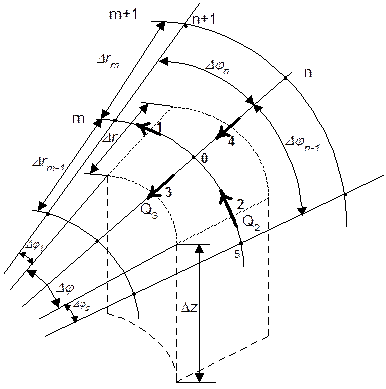
Рисунок 18. – Схема элементарного объема в цилиндрических координатах.
Тогда его объем ΔV=0,5(r3+r4) Δr Δz Δφ. Предположим, что направ- ления тепловых потоков Q = q F соответствуют стрелкам на рисунке, а Δz =1. Уравнение теплового баланса для объема ΔV в общем виде запишется как
dQ = q4 dl4 + q2 dl2 – q1 dl1 – q3 dl3.
Здесь qi – плотности тепловых потоков в точках i, одинаковые по всей ширине dli.
В
разделе 3.5 мы получили формулу q = -
где С =
=
. Следовательно 
.
Если расчетный слой (стенка) цилиндрический или сферический, с малым радиусом кривизны, то для определения q лучше учесть коэффициент формы ζ. Мы же в данном случае будем считать кривизну незначительной, и слой примем в виде простого клина, то есть примем ζ=1. Тогда
С = 
, и q = -
, где δ – расстояние между
изотермами с температурами ti и ti+1.
При известной
функциональной зависимости λ от температуры его усредненные значения 
находятся по формуле,
приведенной в разделе 3.5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.