Тепломассообмен (физико-математические основы): Учебное пособие, страница 35

Наиболее  просты  уравнения  и  условия  однозначности  при  стационарном режиме.  Так, дифференциальное  уравнение  теплопроводнос-  ти  в  этом  случае  имеет  вид

Если    принять  l(¶ t/¶x)  за  одну,  а  х  -  за  другую  переменную,  то  их  легко  разделить:

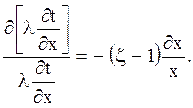
Для   этих  выражений  есть  табличные  интегралы. Если  их  взять  неопределенными,  то 

следовательно,  l(¶ t /¶x) = C/ x ^z-1.   Теперь  снова  можно  разделить  пере-менные   l¶t  и  х:  l¶t = C¶x /x ^z-1.

Стационарный  температурный  режим  тела  сохраняется    в  процессе  теплообмена,  если  тело,  в  котором  нет  стоков  или  источников  тепла,  отдаёт  тепла  столько,  сколько  получает.  Такой  режим  обычно  наблюдается  в  стенах  непрерывно  работающих  печей,  зданий  и  других  инженерных  сооружений.  Они  могут  быть  плоскими,  цилиндрическими  и  сферическими,  причём  цилиндрические  и  сферические  могут  быть  частично.  Температура  по  толщине  таких  стен  при  стационарном  режиме  постоянна  во  времени.

В  качестве  координат  поверхностей  примем   х₁  и  х₂ ,  а  температуры  поверхностей  соответственно  обозначим  через  t ₁  и  t ₂.  Это  будут  граничные  условия  первого  рода  в  их  простейшем  варианте  (постоянные  во  времени).

Теперь  последнее  дифференциальное  уравнение  можно  проинтегрировать  в  пределах  и  получить  выражение  для  константы  С:

Отсюда   .

Договоримся  усреднить  l  таким  образом,  чтобы 

Тогда  средний  коэффициент  теплопроводности  стенки      Здесь  под  интегралом  l - функция    температуры.

Если  в  дифференциальное  уравнение  подставить  значение  константы  С  и  проинтегрировать  его  от  текущей  температуры  t  до,  например,  температуры  t ₂,  то  получится  уравнение  температурного поля                              

, с  помощью  которого  можно  рассчитать   температуру  в  любой  точке  х  по  толщине  стенки. Следует  иметь  в  виду,  что  интеграл  по  х  можно  брать  как  степенной  только  при   ¹2.

При  нестационарном  режиме  решение  того  же  уравнения  теплопроводности  усложняется  в  связи  с  появлением  еще  одной  переменной -  времени  t.  Тогда  приходится  прибегать  к  разделению  температурных  функций,  одна  из  которых  предполагается  зависящей  только  от  координаты,  а  вторая  -  только  от  времени.

Методику разделения  температурных  функций рассмотрим на  примере  симметричного  нагрева (охлаждения)  бесконечной  пластины  в  среде  с  постоянной  во  времени  температурой  t _c,  при  постоянном  коэф-фициенте  теплоотдачи   a.  Примем  теплофизические  свойства  пластины  не  зависящими  от  температуры,  а  начальную  ее  температуру  t_н 

                                                                     примем  одинаковой  по  всей  тол          t _c                                                    t_c          щине. Учитывая  симметричность наг           t_п                                                      рева,  начало  координаты  х  примем 

                                                               в  плоскости  симметрии  пластины

(рисунок  15).

При  толщине  пластины  δ, вследt _ц                                                                      ствие  симметричности  нагрева,  глуs              s                        бина  прогрева  s = δ/2. 

                                                                       Уравнение  теплопроводности

                                                             х     при  нестационарном  температурном

0                              режиме  и  одномерном   температурРисунок  15.- Схема  пластины.         ном  поле  запишется  в  виде

(∂t⁄∂τ) = a (∂²t/∂x²).

Координата  0 ≤ х ≤ s,  то есть  будем  рассматривать  процесс  только  в  одной  половине  пластины,  поскольку  во  второй  распределение  температуры  будет  зеркальным  отображением  такового  в  первой  половине.