Тепломассообмен (физико-математические основы): Учебное пособие, страница 40

С  помощью  таблиц  методом  конечных  интегральных  преобразований  можно  решать  большинство  задач  нестационарной  теплопроводности  не  только  с  одномерным,  но  и  с  двух-  трёхмерным  полем,  с  внутренними  источниками  или  стоками  тепла,  при  любых  граничных  условиях.

Для  иллюстрации  метода  рассмотрим  решение  задачи  о  нагреве(охлаждении) пластины  толщиной  2s,  с одномерным  симметричным  температурным  полем,  при  постоянной  температуре  поверхности  t (s,t)  =   = const  =  t _п .  Теплофизические  свойства  пластины    постоянны, начальная  температура  одинакова  по  всей  толщине  и  равна t _н.  Условия  задачи  можно  сформулировать  следующим  образом:  имеем  дифференциальное  уравнение  (¶t/¶t) = a (¶ ²t/¶x²)  при  условиях  t(x,0) = t _н = const,  t(s,t) = t _п =     = const,  (¶ t/¶x)_x=0 = 0.  Применяя  преобразование  Лапласа  к  уравнению  по  времени  t,  получим  p T(x,p)  -  t(x,0) = a [d ² T(x,p)] /dx² = aT¢¢(x, p).  Таким  образом,  дифференциальное  уравнение  в  частных  производных  для  оригинала  функции  t (x,t)  превращается  в  обыкновенное дифференци-  альное  уравнение  для  изображения  T(x,p),    так  как  последнее  не  зависит  от  времени  t.                                                                                                   Учитывая,  что  t (x,0) = t _н ,  перепишем  уравнение  в  виде  T¢¢(x,p) -        - p[ T(x,p) - (t _н /р)] /а  = 0.  Анализ  показывает,  что  решением  этого уравне-  ния  является  выражение  T(x,p)  -  (t _н/p) = C₁ ch + C₂ sh .

Дополнительные  условия  в  изображениях  будут  иметь  вид:  T¢(х,p) = 0,    T(s,p) = t_п /р.  Из  условия  симметричности

(С₁  sin)×х + (C₂ ch )×х = 0 .

При  x = 0 гиперболический sh (x) = 0,5(exp x - exp (-x)) = 0, гиперболичес-кий ch(x) = 0,5(exp x + exp (-x)) =1, поэтому  С₂ = 0  и,  следовательно,   [T(x,p)  -  (t _н /p)] = C₁ ch(x).

Из граничного условия T(s,p) = (t _н/p) + C₁ ch (s) = t _п/р  находим  С₁=   = - (t_н–t_п)/p ch (s)  и  уравнение  температурного  поля  в  изображени-ях  запишется  в  виде

[ (t _н /р)  -  Т(x,p)]  = (t _н  -  t _п) ch (x) / p ch(s) = F( p) / f(p).

Гиперболические   функции,  как  и  тригонометрические,  разлагаются  в  бесконечные  степенные  ряды  с  показателями  степени  в  виде  натуральных  чисел.  Поэтому  можно  сказать,  что  F(р)/f(р)  есть  отношение  двух  обобщенных  полиномов  -  Ф(р) = (t _н  -  t _п)(1 + x²p/2!a  +  +x⁴p²/4!a² + ×××)  и f (р) = р (1+ S²p/2! a + S⁴p²/4! a² + ××× ),  причём  последний  не  содержит  постоянной,  так  как  р = var.

В  соответствии  со  свойствами  изображений,  они  в  таком  случае    могут  быть  переведены  в  оригинал  с  помощью  теоремы  разложения

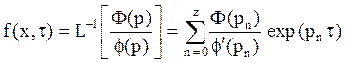
Здесь  p _n – корни  полинома  f(р),  для  нахождения  которых  приравняем       p ch (s) = 0. Получим  простой  корень  р₀ = 0,  а из условия ch (s) =  =cos ( is) = 0   получим  бесконечное  множество  корней

h _n = (2n –1)p/2 = is   при  n = 1,2,3,…¥ .  Отсюда  p _n = - a h_n²/s².  Тогда  производная

f¢(р_n) = [ p_n s /2] sh (s) + ch(s) =

= 0,5 (s) sh (s) + ch (s).

При  р₀ = 0  получаем  f¢(р_n) = 1, ch (x) = 1,  exp (p_n t) = 1,  поэтому  от  первого  члена  суммы  в  f(x,τ)  остаётся  (t _н  -  t _п).