Тепломассообмен (физико-математические основы): Учебное пособие, страница 38

t ₂                        изображается  симметричной  кривой  с  оптимумом (рисунок  16).

                х¢                                    х             Общее   решение  дифференциального  уравнения  теплопроводности,  опи-   

Рисунок  16. – Функция  Т(х,х¢,t)    сывающее  выравнивание  температуры     в  моменты  времени         в  массиве,  получится  как  сумма  всех             t ₁   и    t ₂> t ₁.                 источников  в  плоскости  х¢  (при  t¢=0):

.

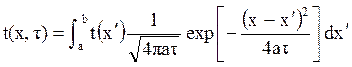В  неограниченном  массиве  пределы  интегрирования  равны   -¥,  +¥,  а  в  полуограниченном  -0,  +¥.

При  двухмерном  температурном  поле

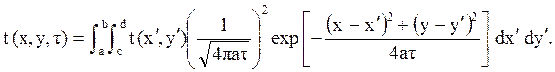
При  непрерывно  действующем  источнике  дифференциальное  уравнение  имеет  вид  (¶t/¶t) = a (¶ ²t/¶x²) + q(x,t)/g c_p,  а  частное  решение  его

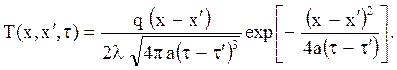
Если    массив  полуограничен,  то  координата  ограничивающей  плоскости  х¢ = 0.  Пусть  начальная  температура  массива  по  всему  объёму  равна   нулю,  а  при  t¢ = +0  в  плоскости  х  она  мгновенно  поднимается  до  t _п  и  далее  остаётся  постоянной  во  времени.  Тепловой  поток,  отнесенный  к  единице  координаты  х,  q = 2lt _п ,   а  общее  решение   дифференциального  уравнения,   то  есть  уравнение  температурного  поля,  будет  иметь  вид

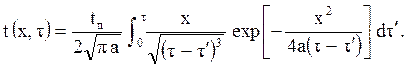
Полученные  зависимости  для  t(x,t)  необходимо  ещё  проинтегри- ровать  по  t¢.  Эту  операцию  рассмотрим  на  примере  предыдущего  уравнения. Положим x = х /.  Тогда   нижний    предел    интеграла   x ₀= х / ( при  t¢= 0),  а  верхний (при t¢= t)  будет  равен  бесконеч- ности; переменная  t¢= t - х ²/4а x ²,  а  dt¢ = 2х² dx/ 4ax ³. После подстанов- ки,  замен  и  преобразований получим  уравнение  температурного  поля

Здесь    -  дополнительный  интеграл  вероятности,  обозна-  чаемый  через  erfc x.  Его   можно  ещё  выразить  через  функцию  ошибок  Гаусса   erf x:  erfcx  = 1 – erf x. При  малых  значениях  x  для  расчётов  удобнее  использовать

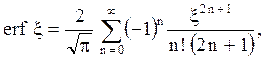
а  при  больших  x  -

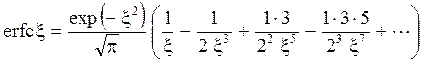
Для  решения  задач  по  теплопроводности  в  объёме  тел  конечных  размеров  можно  использовать  так  называемый  метод  отражений,  суть  которого  заключается  в  подборе  соответствующих  по  форме  и  мощности  источников  тепла  на  границах  тел.  Решения  получаются  сложными,  и  поэтому  метод  отражения  почти  не  используется.

С  помощью  функций  Грина  по  методу  источников  можно  решать  задачи  тепломассопереноса  в  телах  конечных  размеров  при  одно- ,  двух-  и  трёхмерных  полях.  Сложность  их  использования  состоит  в  том,  что  они  не выражаются  определенными  формулами,  как,    например,  функции  Бесселя,  а  их  вид  зависит  от  краевых  условий  задачи.  Поэтому  для  каждого конкретного  случая  функции  Грина  нужно  сконструировать,  для  чего  требуется  математическая  изобретательность.

3.7.    Методы  интегральных  преобразований

Методы  интегральных  преобразований  обладают  рядом  преимуществ  перед  ранее  изложенными  классическими  методами,  а  именно:  они  стандартны,  позволяют  получать  решения  для  одно-,  двух-  и  трехмер- ных полей; использование  таблиц  изображений  и  оригиналов  функций  упрощает  и  ускоряет процесс нахождения  решений. Но эти методы при-  менимы  лишь  к  линейным  уравнениям.

Суть  методов  состоит  в  том,  что  основные  математические  операции  проводятся  не  с  самими  функциями,  определяемыми  условиями  задачи,  а  с  их  видоизменениями  -  изображениями. 

Выражение  F₁(p, x₂, ., x_n) =  называется  интеграль-   ным преобразованием функции  f (x₁, x₂,.. x_n)  по  переменной  х₁.При  этом  F₁(p, x₂,., x_n)  называется  изображением  оригинала  f (x₁,…, x_n),  а  K(p x₁) - -  ядром  интегрального  преобразования.

Интегральные  преобразования  могут  быть  в  конечных  и  в  бесконечных  пределах.

Метод  конечных  преобразований  наиболее  удобен  для  решения  неоднородных  уравнений  параболического  типа  с неоднородными  краевыми  условиями.