При p n = - a h n2/ s2 производная f¢(p n) = [i h n sh ( ih n)] /2 =
= - (h n sin h n)/2 .
Если cos h n = 0, то sin h n = ± 1 = (-1)n+1, f¢(p n) = - h n (-1)n+1/2. Полином
Ф(рn) = (t н – t п) ch (i h n x/s) = (t н – t п) cos (h nX), X = x/s.
Таким образом, правая часть уравнения температурного поля в оригинале будет иметь вид
(t
н – t п ) – (t
н – t п) ![]()
Левая же часть после обратного преобразования получится в виде
L-1[ (t н /p) – T(x,p)] = t н – t (x, t).
Таким образом, в оригинале уравнение температурного поля будет иметь вид
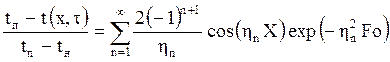
Как видно из этого примера, для решения задач, кроме таблиц, нужно знать некоторые свойства преобразований. Начинающим лучше всего познакомиться с этими свойствами и поучиться пользоваться ими на примерах в [2] , где приведены решения уравнения теплопроводности при различных граничных условиях как методами разделения переменных, так и методами интегральных преобразований.
Кроме точных методов решения дифференциальных уравнений в частных производных имеется ряд приближенных аналитических методов, на которых мы останавливаться не будем в связи с ограниченным временем, тем более, что изложение этих методов даже более громоздко, чем объяснение точных, а распространения широкого они не получили.
3.8. Численные методы
С появлением быстродействующей вычислительной техники, обладающей большим объёмом памяти, для исследования и расчётов процессов тепло- и массопереноса всё более широко применяются численные методы: метод сеток (конечных разностей), конечных элементов, зональные. Их названия говорят о том, что они имеют одну и ту же основу – малые изменения параметров процессов во времени и в пространстве. Отличия их определяются областями применения и особенностями таких процессов как аэродинамика, теплообмен излучением, упругие деформации, особенно в телах сложной формы.
Наиболее универсальным и разработанным к настоящему времени является метод конечных разностей, позволяющий решать как линейные так и нелинейные дифференциальные и интегродифференциальные уравнения переноса массы и энергии. Его использование позволяет отказаться от упрощений математической модели процессов, причём решение может быть получено с любой наперёд заданной точностью. Большим достоинством этого метода является также осуществление расчётов путём многократного повторения одинаковых математических операций, что упрощает разработку машинных программ.
Метод конечных элементов предпочтителен при расчётах процессов в системах сложной геометрической формы.
Зональный метод близок по форме к методу конечных элементов, но применяется для расчётов лучистого теплообмена между телами, в том числе и при участии полупрозрачных сред.
3.8.1. Метод конечных разностей
Сущность метода конечных разностей заключается в том, что в исходном дифференциальном уравнении, или в системе уравнений, а также в условиях однозначности, бесконечно малые (неопределенные) величины заменяются величинами малыми, но конечными (имеющими определенную величину). В общем виде эта замена не представляет труда. Например, уравнение теплопроводности в дифференциальной форме (¶ t/¶t) = a (¶ 2t/¶x2) изменяется только за счёт одного символа ¶, который заменяется символом D, то есть уравнение приобретает вид (Dt/Dt) = a(D2t/Dx2). Но теперь это уравнение стало алгебраическим, так как входящие в него величины должны иметь определенные числовые значения, и позволяющим получить приближенный результат. Замена дифференциальных уравнений конечно – разностными уравнениями может быть осуществлена несколькими способами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.