Тепломассообмен (физико-математические основы): Учебное пособие, страница 37

Полученное   таким  же  образом   уравнение  температурного  поля  для  шара   тоже  выражается  через  функции  синуса  и  косинуса,  а  уравнение  для  цилиндра  -  через  функции  Бесселя,  графическим  изображением  которых являются  затухающие  в  бесконечности  гармоники.              

Если   использовать  обобщенные  функции

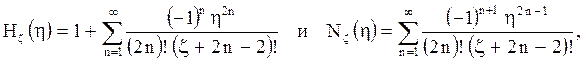                      в которых z - коэффициент  формы  канонических  тел (пластины,  цилиндра  и  шара),  то  для  всех  можно  получить  одно  обобщенное  уравнение  температурного поля   в  виде

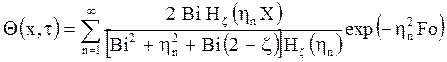
с характеристическим уравнением      в  котором  при  z =1(пластина) H₁(Ф) =cos Ф, N₁(Ф) = sin Ф ; при z =2 (цилиндр) Н₂(Ф) =J₀(Ф),  N₂(Ф) = J₁(Ф);  при  z = 3(шар)  Н₃(Ф) = (sin Ф)/Ф, N₃ = (sin Ф – cos Ф)/Ф².   Функции эти  также  обладают  свойством  ортогональности.

Из  уравнений  температурных  полей  третьего  рода  можно  получить  уравнения  для  граничных  условий  первого  рода,  если  принять a = ¥  а  l = 0. Тогда из уравнения теплообмена следует, что t _с= t _п (такое  выравнивание  температур подтверждается  опытом),  поэтому  Q(x,t) = (t _п – t)/(t _п  - t _н).Число Bi = ¥,  а  h _n= (2n – 1) p /2. Поэтому cos h _n =  = 0,  sin h _n = (-1)ⁿ⁺¹

Упрощается  уравнение  температурного  поля  и  при  Bi,  близком  к  нулю,  потому  что  тогда  перепад  температур  по  толщине  тела  близок  к  нулю,  и  им  можно  пренебречь,  считая  температуру  одинаковой  по  всей  толщине.  В  этом  случае  тело  называют  термически  тонким,  а  при  большом  перепаде  -  термически  массивным.

Приведенное   решение  для  симметрично  нагреваемой  пластины  показывает, что  применение  метода  разделения  переменных  предполагает  хорошее  знание  свойств  различных  функций,  которые  приходится  подбирать  для  решения  того  или  иного  дифференциального  уравнения . Ещё  большие  затруднения  возникают  при  решении  задач  конвективного  тепло-  и  массопереноса .  В  настоящее  время  их  решение  возможно  только  при  простых  начальных  и  граничных  условиях.

Кроме  того,  метод  разделения  в  большинстве  случаев  нельзя  применять  для  полуограниченных  и  неограниченных  тел;  нельзя  непосредственно  применять  при  неоднородных  граничных  условиях;  трудно  использовать  его  при  граничных  условиях  четвёртого  рода.

3.6 .  Метод  источников

Физическая  сущность  этого  метода  состоит  в  том,  что  любой  процесс  распространения  тепла  в  теле  можно  представить  как  совокупность  процессов  выравнивания  температуры,  вызываемых  действием  множества  элементарных  источников  тепла,  распределенных  как  в  пространстве,  так  и  во  времени.  Решение  задач  этим  методом  сводится  в  основном   к  правильному  выбору  источников  и  их  распределения.  Метод  особенно  удобен  при  решении  задач  для  неограниченных  и  полуограниченных  тел.  Примером  таких  задач  могут  быть  нестационарные  процессы  в  почве,  без  её  замерзания,  при  изменении  внешних  условий,  а  также  в  металле  при  сварке  и  резке  его  дугой  или  пучком  электронов, при  нагреве его вихревыми токами.

В  неограниченном  плоском  массиве   с  постоянными  теплофизическими  свойствами,  без  источников  и  стоков  тепла  температурное  поле,  как  известно,  описывается  дифференциальным  уравнением  (¶t/¶t) = а(¶ ²t/¶x ²),  имеющим,  оказывается,  ещё  одно  частное  решение,  которое  называется  фундаментальным:

.

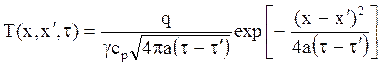В  этой  формуле  q = gc_pt(x¢)dx – количество  тепла  в  плоском  слое  толщиной  dx.  Оно  рассматривается   как  мгновенно  действующий  точечный 

                                                         источник,   сосредоточенный  в  плоскос-

t ₁                           ти  х¢  в  момент  времени  t¢. 

Распределение  температуры,  описываемое  функцией  Т(х,х¢,t)  точечного 

                                                          мгновенного  источника,  графически