Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела

Глава 2

КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

В этой главе изучаются геометрические свойства движения сплошных сред без учёта их физических свойств, действующих сил и других причин, вызывающих деформацию сплошной среды. Задача ставится следующим образом: даны положения точек среды до и после деформации, требуется определить вызванные деформацией изменения расстояний между точками и ориентацию в пространстве отрезков, соединяющих бесконечно близкие точки сплошного тела. Вопрос этот чисто геометрический. Поэтому результаты, полученные в настоящей главе, применимы к любым телам и средам: твёрдым, жидким, газообразным а также к физическим полям.

2.1. Способы изучения движения деформируемых сред

2.1.1. Системы координат

Любое механическое движение представляет собой происходящее в пространстве и времени изменение положения тел и отдельных их точек относительно других тел. Движение всегда определяется в некоторой системе отсчёта – системе координат. В механике сплошных сред используются две системы координат: пространственная и материальная. Пространственная система координат жёстко привязана к телу, относительно которого определяется движение сплошной среды. Материальная система координат жёстко привязывается к точкам изучаемой сплошной среды и вместе с последней изменяет своё положение в пространстве и времени.

Выбор системы координат произволен и определяется соображениями удобства при изучении движения деформируемого тела. Пространственная система координат может быть декартовой прямоугольной системой, цилиндрической, сферической или иной другой. Так, например, в исследовании поведения оболочечных тел большие преимущества доставляет криволинейная ортогональная система координат, координатные линии которой совмещают с линиями главной кривизны характерной поверхности оболочки. Единственным ограничением является требование, чтобы пространственная система координат была инерциальной, т.е. такой, чтобы в ней выполнялся первый закон Ньютона (закон инерции). При выполнении этого требования для описания сплошных сред полностью применимы второй и третий законы Ньютона. На практике очень часто за точку отсчёта (за начало координат) принимается точка, неподвижная относительно Земли (геоцентрическая система отсчета). В этом случае система координат приближённо может считаться инерциальной

Материальная система координат, непосредственно привязанная к изучаемому телу, позволяет наиболее простым образом следить за движением его отдельных точек. В материальной системе координат все точки изучаемого тела имеют не изменяющиеся с течением времени координаты. Деформируемое тело как бы покоится относительно материальной системы координат. Вместе с деформацией тела деформируется материальная система координат: координатные линии растягиваются, сжимаются, извиваются, изменяют ориентацию в пространстве. Координатные линии материальной системы координат, как правило, в начальный момент времени совпадают с координатными линиями пространственной системы. Однако с течением времени они получают существенные отклонения от последних. Так,  например, будучи в  начальный момент времени декартовой системой  координат в любой другой момент времени она превращается в криволинейную не ортогональную систему. Важной особенностью материальной системы координат является то, что математическая запись любой линии или поверхности в этой системе координат сохраняется справедливой в течение всего времени изучения поведения деформируемого тела.

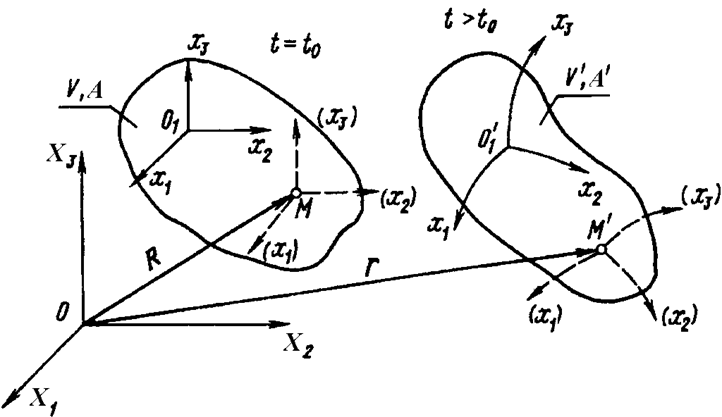
На рис. 9 представлена пространственная система координат в виде декартовой прямоугольной системы , относительно которой исследуется движение деформируемого тела. В начальный момент времени t = t₀  деформируемое тело имеет объём V, поверхность которого равна А. В рассматриваемом теле зафиксирована произвольная точка М, координаты которой обозначены следующим образом: Х₁ = х_1,  Х₂ = х_2,  Х₃ = х_3.  Через точку М проведены координатные линии материальной системы координат параллельно координатным осям пространственной системы, которые обозначены так же, как и координаты точки М, т.е. х_1,  х_2,  х_3. Справа показано положение этого же тела в какой-то момент времени t > t₀. Изменились объём тела, его поверхность и положение рассматриваемой точки, которые обозначены соответственно через  Координатные линии  материальной  системы  координат искривились и изменили свою ориентацию.

Рис. 9. Координатные линии материальной системы координат при t=t₀ и t>t₀.

Пространственную систему координат часто называют системой отсчёта наблюдателя, а материальную систему – сопутствующей системой отсчёта.

2.1.2. Перемещение деформируемого тела