Министерство образования Российской Федерации
Дальневосточный государственный технический университет
(ДВПИ им. В.В. Куйбышева)
Кафедра прикладной математики и механики
Курсовая работа
по математической физике.
Выполнил:
Проверил:
Оценка:
Владивосток
2011 г.
ОГЛАВЛЕНИЕ
Стр.
1. Метод разделения переменных(метод Фурье)……...………………………..2
Пример №2 Приведение уравнения к каноническому виду ……………….6
Пример №2(реализация в пакете Maple приложение 1)
Аналитическое решение………………………………………………………8
Пример №3 Метод разделения переменных………………………………..10
2. СПИСОК ЛИТЕРАТУРЫ……………………………………………….........12
Рассмотрим первую краевую задачу для однородного уравнения колебаний струны
![]() (1)
(1)
![]()
![]()
![]() (2)
(2)
![]()
![]()
Где ![]() - это
начальный прогиб, а
- это
начальный прогиб, а ![]() -
это начальная скорость колебаний струны. Согласно методу Фурье будем искать
решение уравнения в виде произведения 2-х функций:
-
это начальная скорость колебаний струны. Согласно методу Фурье будем искать
решение уравнения в виде произведения 2-х функций:
![]()
![]() (3)
(3)
Подставим (3) в (1):
![]() |:
|:![]()
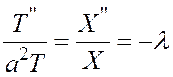
![]()
![]()
Подставляем (3) в граничные условия (2):
![]()
![]()
Требуется найти такие значения ![]() , при
которых данная задача имеет ненулевое решение. Эти значения
, при
которых данная задача имеет ненулевое решение. Эти значения ![]() называются
собственными значениями задачи, а соответствующие им решения – собственными
функциями.
называются
собственными значениями задачи, а соответствующие им решения – собственными
функциями.
Задача на собственные значения называется задача Штурма–Леувиля:
1) ![]() <0
<0
![]()
![]()
![]()
![]() - корни вещественные и
разные
- корни вещественные и
разные
![]()
![]()
(так как выражение в скобках не равно 0)
При ![]() <0
только нулевые решения.
<0
только нулевые решения.
2) ![]()
![]()
![]()
![]()
![]()
(так как l не равно нулю)
3) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
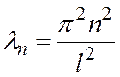
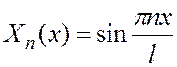
-собственная функция.
Так как уравнения и граничные условия однородные, то собственные функции определяются с точностью до постоянного множителя, т.е. функция СXn(x) так же являются собственными.
![]()
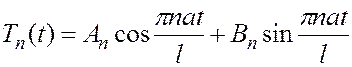
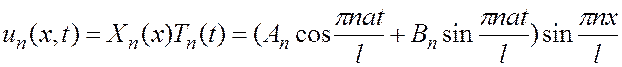
Будем искать общее решение в виде суммы ряда:
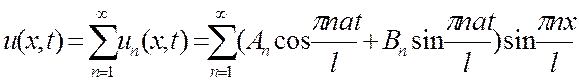 (5)
(5)
- равномерно сходящийся.
![]()
Ряд (5) сходится равномерно, если
сходится числовой ряд 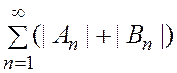 согласно
признаку равномерной сходимости Вейерштрасса.
согласно
признаку равномерной сходимости Вейерштрасса.
Подставляем (5) в начальные условия:
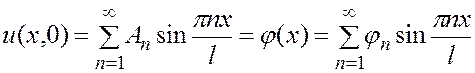
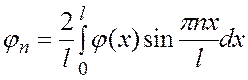
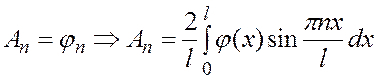 (6)
(6)
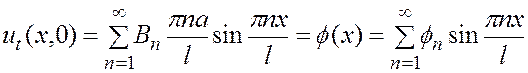
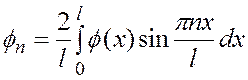
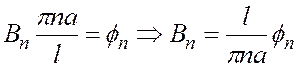
Ряд (5) вместе с (6) дает нам решение задачи:
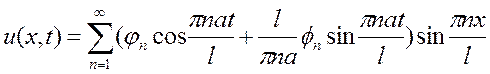
![]() определяют
поведение коэффициентов An и Bn.
определяют
поведение коэффициентов An и Bn.
Свойства коэффициентов Фурье.
![]()
![]()
Если функция ![]() имеет
непрерывную производную k, то её коэффициент Фурье
имеет
непрерывную производную k, то её коэффициент Фурье 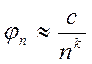 , где с –
некоторая константа. Таким образом, чтобы решение (5) можно было
дифференцировать 2 раза, необходимо чтобы
, где с –
некоторая константа. Таким образом, чтобы решение (5) можно было
дифференцировать 2 раза, необходимо чтобы ![]() имело
непрерывную производную 3 порядка, а
имело
непрерывную производную 3 порядка, а ![]() 2
порядка. Если условие для
2
порядка. Если условие для ![]() не
выполнено следует рассматривать сходимость ряда Фурье в обобщенном смысле.
не
выполнено следует рассматривать сходимость ряда Фурье в обобщенном смысле.
Пример №1.
> restart;
> yr:=9*diff(u(x,y),x,x)+6*diff(u(x,y),x,y)+1*diff(u(x,y),y,y)-9*diff(u(x,y),x)-3*diff(u(x,y),y)=0;
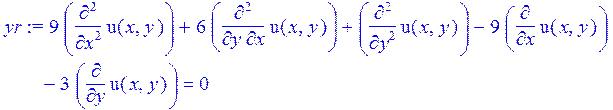
> yr1:=lhs(yr);
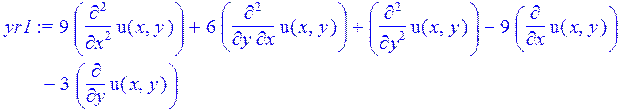
> a11:=coeff(yr1,diff(u(x,y),x,x));
![]()
> a12:=coeff(yr1,diff(u(x,y),x,y))/2;
![]()
> a22:=coeff(yr1,diff(u(x,y),y,y));
![]()
> x_yr:=a11*z^2+2*a12*z+a22=0;
![]()
> res1:=solve(x_yr,z);
![]()
> xi:=y-int(res1[1],x);
![]()
> eta:=x;
![]()
> xix:=diff(xi,x);
![]()
> xiy:=diff(xi,y);
![]()
> xixx:=diff(xi,x,x);
![]()
> xiyy:=diff(xi,y,y);
![]()
> xixy:=diff(xi,x,y);
![]()
> etax:=diff(eta,x);
![]()
> etax:=diff(eta,x);
![]()
> etay:=diff(eta,y);
![]()
> etaxx:=diff(eta,x,x);
![]()
> etayy:=diff(eta,y,y);
![]()
> etaxy:=diff(eta,x,y);
![]()
> Uxx:=u[xixi]*xix^2+2*u[xieta]*xix*etax+u[etaeta]*etax^2+uxi*xixx+ueta*etaxx;
![]()
> Uxy:=u[xixi]*xix*xiy+u[xieta]*(xix*etay+xiy*etax)+u[etaeta]*etax*etay+uxi*xixy+ueta*etaxy;
>
![]()
> Uyy:=u[xixi]*xiy^2+2*u[xieta]*xiy*etay+u[etaeta]*etay^2+uxi*xiyy+ueta*etayy;
![]()
> Ux:=u[xi1]*xix+u[eta1]*etax;
![]()
> Uy:=u[xi1]*xiy+u[eta1]*etay;
![]()
> yr2:=subs({diff(u(x,y),x,x)=Uxx,diff(u(x,y),x,y)=Uxy,diff(u(x,y),y,y)=Uyy,diff(u(x,y),x)=Ux,diff(u(x,y),y)=Uy},yr);
![]()
Пример №2.
> restart;
> ur:=diff(u(x,t),t$2)=a^2*(diff(u(x,t),x$2))+g;
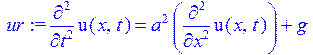
> u(x,t):=v(x)+w(x,t);
![]()
> ur;
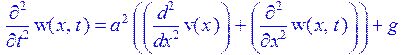
> urv:=diff(v(x),x$2)=-g/a^2;
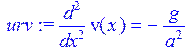
> v(x):=rhs(dsolve({urv,v(0)=0,D(v)(l)=0},v(x)));
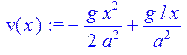
> ur:=expand(eval(ur));
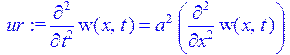
> w(x,t):=X(x)*T(t);
![]()
> ur:=eval(ur)/w(x,t)/a^2;
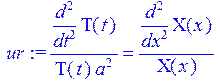
> rhs(ur)=-la^2;
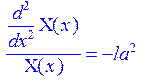
> dsolve({%,X(0)=0},X(x));
![]()
> la:=Pi/2*(2*n+1)/l;
X(x):=sin(la*x);
![]()
![]()
> T(t):=rhs(dsolve(lhs(ur)=-la^2,T(t)));
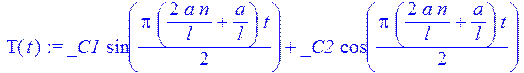
> T(t):=subs(_C1=B,_C2=A,T(t));
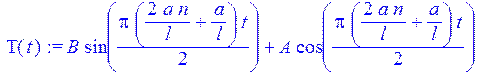
> w(x,t):=Sum(eval(w(x,t)),n=0..m);
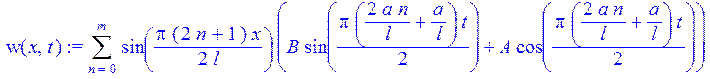
> w(x,0):=eval(w(x,t),t=0)=-v(x);
A:=2/l*int(X(x)*rhs(w(x,0)),x=0..l);
sin(Pi*n):=0;
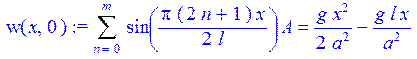
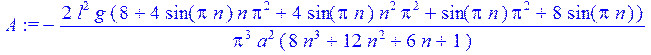
![]()
> A;
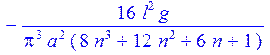
> w[t](x,0):=eval(diff(w(x,t),t),t=0)=0;
B:=2/l/(Pi*(2*a/l*n+a/l)/2)*int(X(x)*rhs(w[t](x,0)),x=0..l);
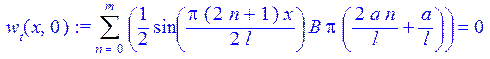
![]()
> u(x,t):=eval(w(x,t)+v(x));
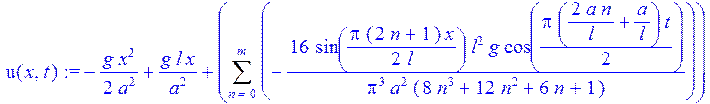
Пример № 3.
> restart;
> v(x):=sin(x)/a^2-x*cos(l)/(l*a^2);
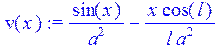
> lambda[n]:=(Pi/2*(2*n+1))/l;
![]()
> A[n]:=-2/l*int(v(x)*sin(Pi/2*l)*x*(2*n+1),x=0..l);
>
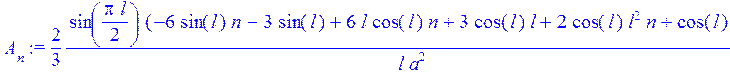
> w(x,t):=Sum(A[n]*cos(lambda[n]*a*t)*sin(lambda[n]*x),n=0..10);
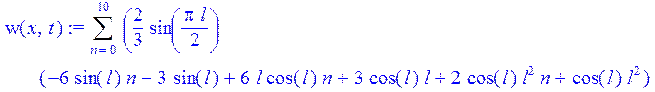
![]()
>
> u(x,t):=v(x)+w(x,t);
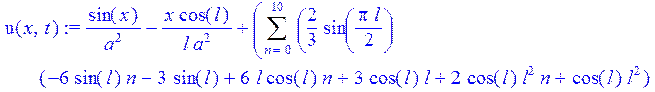
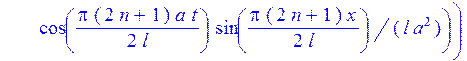
> l:=7;
![]()
> a:=1;
![]()
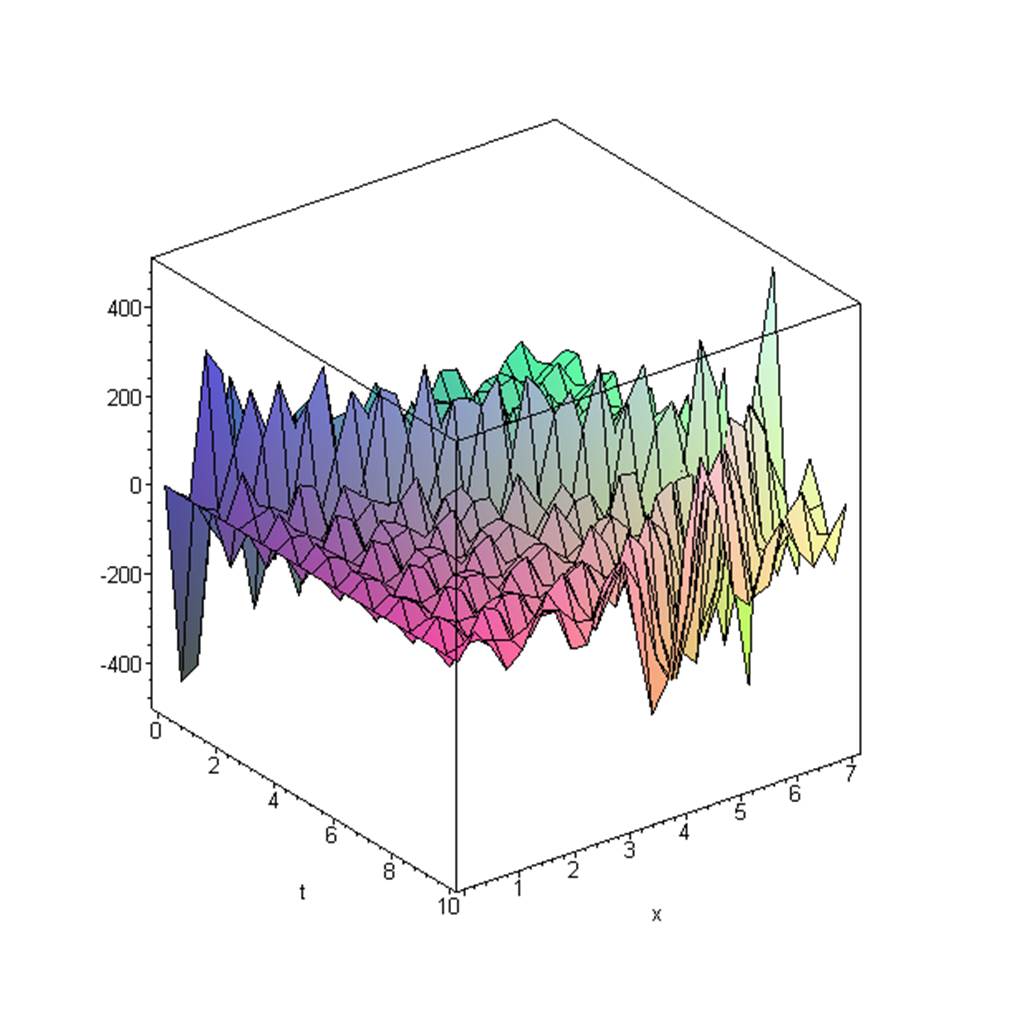
> plot3d(u(x,t),t=0..10,x=0..l);
>
>
>
>
>
Список литературы
1. «Математическая физика (конспект лекций)»
Бочарова А. А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.