Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 13

В результате интегрирования в дополнение к величинам  (2.58) появились еще три константы . Под криволинейным интегралом оказались производные от компонент тензора вращений , которые легко выражаются через компоненты тензора деформаций. С помощью (2.23) получим

       .

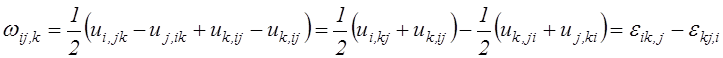Тем самым найдём тождество

.                                                  (2.61)

Подставив (2.60) и (2.61) в (2.58), получим следующее выражение для перемещений точек кривой линии М₀М:

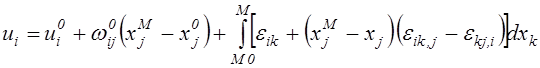.                  (2.62)

Выражение (2.62) впервые было установлено итальянским математиком Э.Чезаро.

Поскольку перемещения точки М не может зависеть от кривой М₀М, то и криволинейный интеграл (2.62) также не должен зависеть от пути интегрирования. Последнее выполняется только в случае, когда под интегралом содержится полный дифференциал. Если ввести обозначения

,       (2.63)

то для независимости криволинейного интеграла от пути интегрирования необходимо и достаточно, чтобы выполнялось следующее условие существования полного дифференциала:

.                                                         (2.64)    

Подставим в условие (2.64) выражения (2.63) 

После сокращения одинаковых слагаемых получим

Так как в общем случае , то

.                                         (2.65)

Равенства (2.65) и определяют искомые условия, которым должны удовлетворять функции  при определении перемещений . Из 81 уравнения (2.65) независимыми являются только шесть. Положив , получим из (2.65) одно из независимых уравнений

.                                                (2.66)

Другое независимое уравнение найдём из равенства (2.65), приняв значения индексов:

.                                           (2.67)

Четыре оставшиеся независимыми уравнения находятся из уравнений (2.66) и (2.67) путём круговой перестановки индексов 1–2–3–1. При других комбинациях индексов равенство (2.65) выполняется тождественно.

Дифференциальные уравнения (2.66), (2.67) путем круговой перестановки индексов носят названия: условия сплошности тела, условия сплошности деформаций, уравнения неразрывности деформаций и т.п. Их также называют уравнениями Сен-Венана, по имени французского ученого, который получил их впервые (1860 г.). Выполнение уравнений (2.65) или (2.66), (2.67) обеспечивает сохранение сплошности односвязного однородного тела при малых деформациях и малых приращениях перемещений. Подстановка компонент тензора деформаций (2.54), выраженных через перемещения, обращает уравнения сплошности (2.65) – (2.67) в тождества .

При существенных приращениях относительных перемещений уравнения сплошности оказываются чрезмерно громоздкими и потому не находят практического применения. С ними можно ознакомится в книге В.В. Новожилова [9]. При необходимости в случае существенных приращений относительных перемещений используются уравнения сплошности в смешанной форме, которая находится путём подстановки в уравнения (2.65) компонентов тензора деформаций с умножением нелинейных членов на минус единицу. Естественно, что при подстановке компонентов тензора деформаций полученные таким образом уравнения обращаются в тождества.

2.11.2. Условия сплошности многосвязных и неоднородных тел

Применительно к многосвязным телам, у которых имеются внутренние полости, не соединенные с внешней поверхностью, для обеспечения сплошности тела при деформации кроме (2.65) требуются дополнительные условия. Это связанно с тем, что при определении деформированного состояния применяется прием превращения многосвязного тела в односвязное путём проведения мнимых разрезов, соединяющих наружную поверхность с внутренними полостями. Дополнительные условия сплошности записываются в виде:

                                                          (2.69)

где индексами минус и плюс помечены перемещения произвольной точки мнимого разреза с обоих сторон от поверхности разреза.