Кинематика сплошной среды. Способы изучения движения деформируемых сред. Перемещение деформируемого тела, страница 4

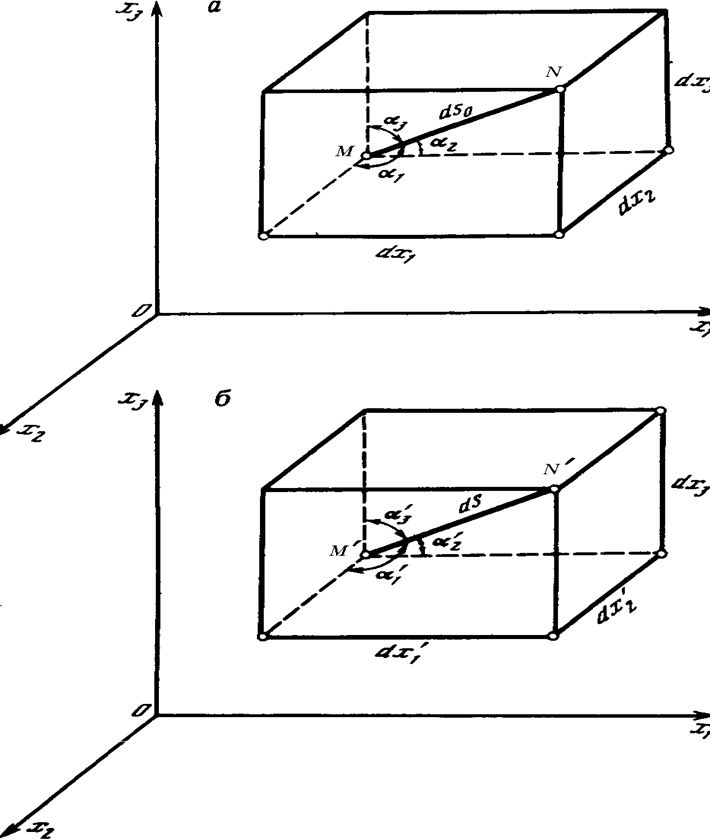
Рис. 11. Определение положения отрезка MN до (а) и после деформации (б)

Введём в рассмотрение символ Кронекера , который определяется следующим образом:

  

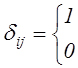
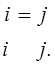
Символ Кронекера позволяет представит квадрат расстояния  в виде: Из девяти слагаемых последнего представления не равными нулю будут лишь те три, у которых i = j. Следовательно  Для представления квадрата расстояния     в требуемом виде обратим внимание на то, что в любой момент времени t = const:  Отсюда  и  Образуя разность квадратов расстояний между точками M и N до и после деформации, находим, что

Введя обозначение

,                                                  (2.7)

перепишем последнее выражение в следующем эквивалентном виде:

                                              (2.8)

Так  как  то  а  В результате  величины   выражаются  через компоненты перемещений:

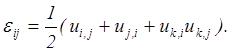                                                                 (2.9) 

Свяжем параметры  с относительной линейной деформацией e. С этой целью умножим равенство (2.5) на сумму   и проведём следующие преобразования:  

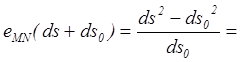
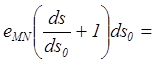
Привлекая равенство (2.8), найдём, что

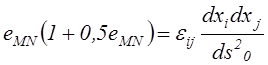.                                       (2.10)

Из рис. 11 видно, что

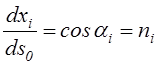,                                                   (2.11)

где через n_i обозначены косинусы углов, образованные отрезком MN с координатными осями  Ох_i  пространственной системы координат в начальный момент времени. Они называются направляющими косинусами отрезка MN, определяя ориентацию этого отрезка в пространстве. С помощью направляющих косинусов формула (2.10) приводится к виду:

.                                            (2.12)

Если отрезок MN до деформации параллелен оси x_i, то лишь один направляющий косинус отличен от нуля и равен единице, остальные направляющие косинусы равны нулю. Например, для оси х₁ имеем: n₁=1, n₂ = n₃ = 0 и формула (2.12) даёт следующее значение линейной деформации для отрезка MN параллельного оси x_i:

.                                              (2.12')

Отсюда:

.                                                 (2.13)

По аналогии определяются относительные линейные деформации элементарных отрезков, параллельных другим координатным осям:

                               (2.13')

Таким образом, формула (2.12) позволяет определить относительную линейную деформацию в любой точке деформируемого  тела по любому произвольному направлению, исходя из геометрических параметров сплошной среды  независимо от её физических свойств. Поэтому эта формула справедлива для любого сплошного тела: твёрдого, жидкого и газообразного. Её также можно применить для описания кинематики любых физических полей.

2.3. Изменение направления линейного элемента. Формула

преобразования локального базиса лагранжевой системы

 координат

2.3.1. Изменение направления линейного элемента

Рассмотрим изменение направления бесконечно малого линейного элемента MN относительно пространственной системы координат в процессе деформации тела. Пусть направление отрезка MN в пространстве до деформации определяется направляющими косинусами n_i (2.11). После деформации отрезок MN займёт положение , образуя с осями пространственной системы координат углы, косинусы которых, как это видно из рис. 11б, равны

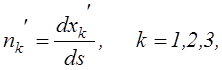                                             (2.14)

где     

Подставив полученное выражение дифференциала   в формулу  (2.14), найдём что

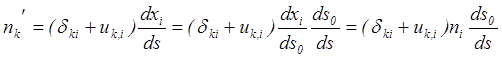
На основании определения относительной деформации (2.5) имеем

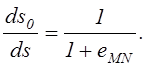
Это равенство позволяет записать формулу, определяющую направляющие косинусы для произвольного направления в точке М после деформации в виде:

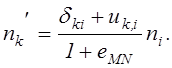                                                   (2.15)

Определим с помощью формулы (2.15) направляющие косинусы отрезка MN после деформации тела для направлений, которые до деформации были параллельны координатным осям. Если отрезок MN до деформации совпадал с направлением оси x₁, то его направляющие косинусы будут равны: Тогда по формуле (2.15) найдём, что после деформации его направляющие косинусы окажутся равными